Question 1

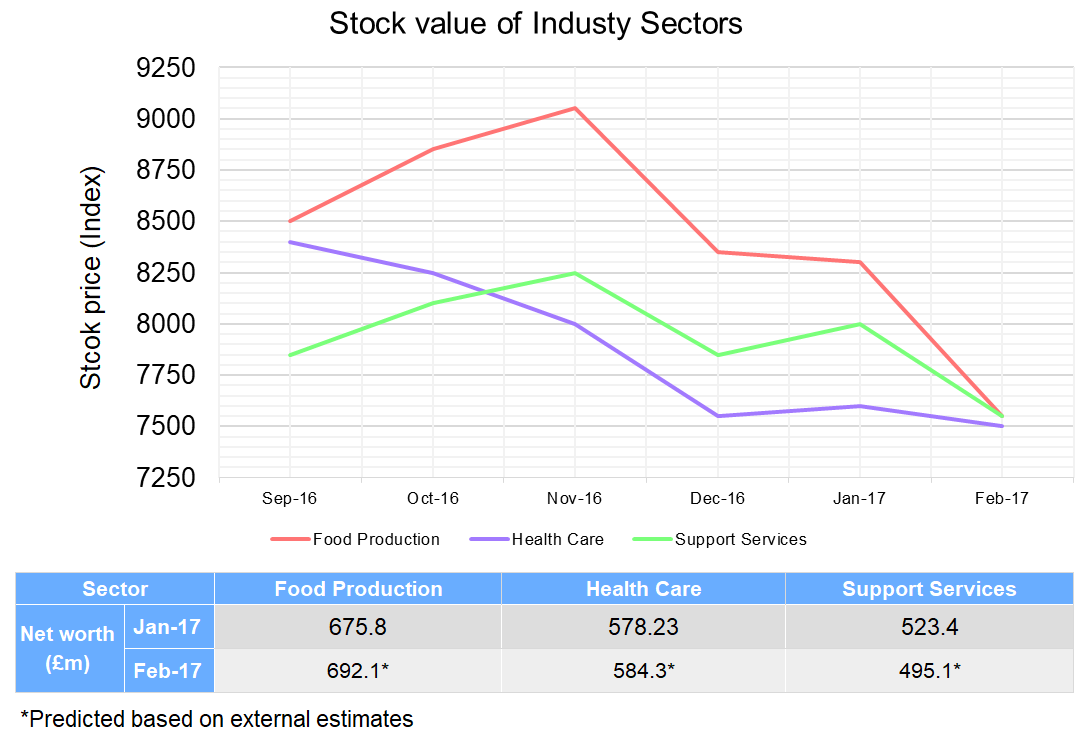
Given that costs of 12% on all valuation above £235m must be paid and based on the net worth of Food production in January 2017, what was the approximate net worth of Food production in November 2016 if stock price trends can be followed.

                A: £677m

                B: £635m

                C: £438m

                D: £590m

Written Solutions

Step 1: We want to use the change in stock price to give an estimate for the value of food production. To do this we will calculate the percentage change in stock price from November 2016 to January 2017.

\dfrac{\text{Jan 16 - Nov 16}}{\text{Nov 16}}=\dfrac{8300-9050}{9050} \times 100 = 8.3\% \text{ decrease}

Step 2: A decrease of 8.3% from November to January corresponds to a multiplier of 0.917. Since we want to reverse this and estimate from January to November we need to divide by 0.917.

\dfrac{\pounds675.8\text{m}}{0.917}\approx \pounds737\text{m}

Step 3: Finally, we need to consider the cost on valuation. Subtract the £235m and take away 12% ( a multiplier of 0.88) from the remaining value.

\pounds737\text{m} - \pounds235\text{m} = \pounds502\text{m}

\pounds502\text{m} \times 0.88 \approx \pounds442\text{m}

Now add the £235m back on to get £677m.

Question 2

Predict the total of all three stock prices in March based on the downwards trend from November to February.

                A: 19,100

                B: 19,400

                C: 20,200

                D: 21,800

Written Solutions

Step 1: Calculate stock price totals for November and February.

\begin{aligned}\text{November: }&9,050+8,250+8,000 = 25,300 \\ \text{February: }& 7,550 + 7,550 + 7500 = 22,600 \end{aligned}

Step 2: Calculate the percentage change from November to February.

\dfrac{22,600 - 25,300}{25,300} \times 100 = 10.7\%\text{ decrease}

Divide by three to find an approximate percentage decrease per month of 3.6%.

Step 3: Finally calculate an estimate for the total of all thre stock prices by using the multiplier that corresponds to a 3.6% decrease, 0.964.

22,600 \times 0.964 \approx \bold{21,800}

Question 3

What is the approximate difference between the predicted net worth of all three sectors combined in February 2017 compared to the actual net worth in February 2017 based on the trend from January 2017?

                A: £90m

                B: £85m

                C: £87m

                D: £92m

Written Solutions

Step 1: To calculate the net worth in February we need to investigate the percentage decrease overall from January to February. First calculate the total of all three stocks for each month.

\begin{aligned}\text{January: }&8,300+8,000+7,600 = 23,900 \\ \text{February: }& 7,550 + 7,550 + 7500 = 22,600 \end{aligned}

Now calculate the percentage change between the two months

\dfrac{22,600 - 23,900}{23,900} \times 100 = 5.4\%\text{ decrease}

Step 2: A 5.4% decrease corresponds to a multiplier of 0.946. We apply this to the total net worth in January 2016 to get the February figures.

\text{January net worth } = 675.8 + 578.23 + 523.4 = \pounds1,777.43\text{m}

\pounds1,777.43\text{m} \times 0.946 = \pounds1,681.45\text{m}

Step 3: Add up the predicted February figures to get £1,771.5m and find the difference.

 1,771.5-1,681.45 \approx \bold{\pounds90\text{m}}

Question 4

What is the total rise in price of stocks over the period as a proportion of the total fall in price?

                A: 32.6%

                B: 34.4%

                C: 35.4%

                D: 33.8%

Written Solutions

Step 1: Identify all price rises and find the sum of these values.

Food Production rises from September to November by a total of 550 points

Health Care rises from December to January by 50 points

Support Services rise from September to November by 400 points, and December to January by 150 points for a total of 550 points.

The total of all price rises is 1150 points.

Step 2: Identify all price decreases and the sum of these values.

Food Production falls from November to December by 700 points, and again from January to February by 750 points for a total of 1450 points.

Health Care falls from September to December by 850 points, and again from January to February by 100 points for a total of 950 points

Support Services fall from November to December by 400 points, and again from January to February by 450 points for a total of 850 points.

The total of all price falls is 3250 points.

Step 3: Calculate the proportion of price rises over price falls.

\dfrac{1150}{3250} \times 100 \approx \bold{35.4\%}

Question 5

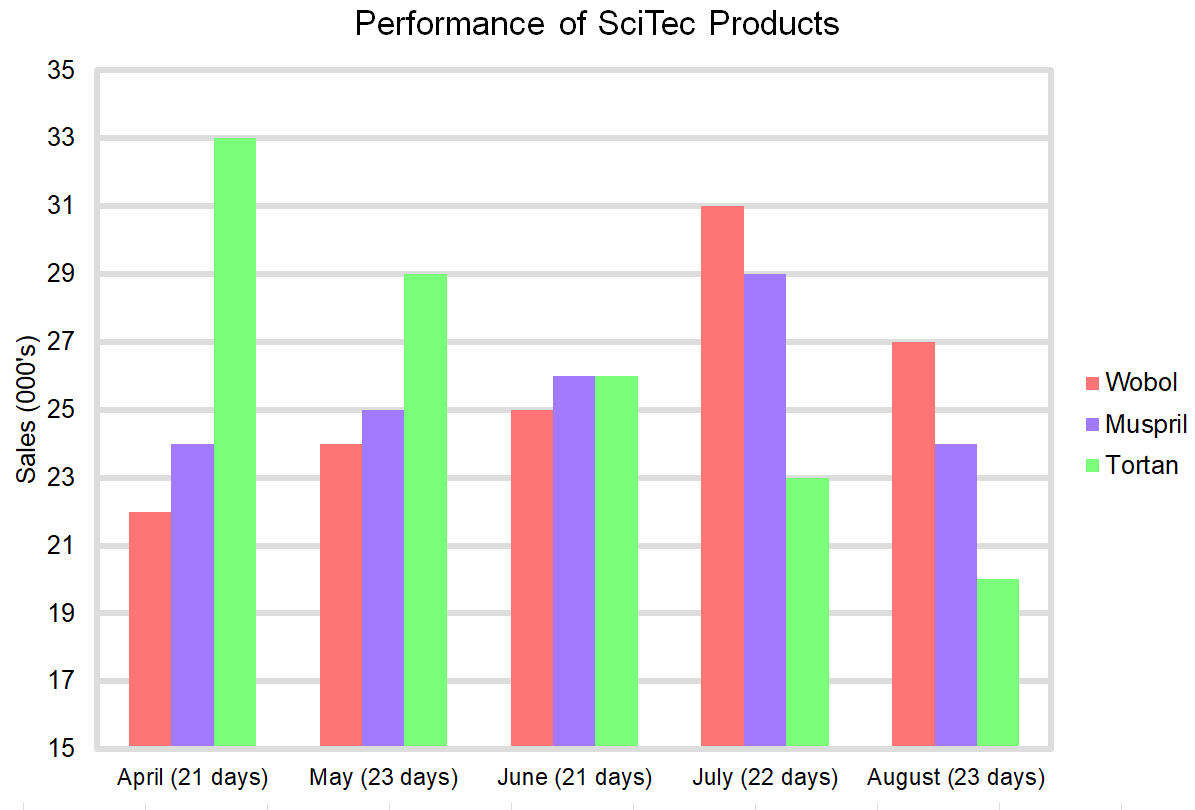
What was the percentage change in sales per day of Muspril from April to May?

            A: 4.7% decrease

            B: 4.9% increase

            C: 5.1% increase

            D: 4.3% decrease

Written Solutions

Step 1: Identify the sales of Muspril for April and May, then divide by the number of days in each month to calculate the sales per day.

\begin{aligned}\text{April: }&24,000\div 21 = 1,143 \\ \text{May: }&25,000 \div 23 = 1,089 \end{aligned}

Step 2: Calculate the percentage change.

\dfrac{May - April}{April}=\dfrac{1,089 - 1,143}{1,089} = -0.047 \text{ or a }\bold{4.7\%\text{ decrease.}}

Question 6

If Wobol sells at £12, Muspril at £10 and Tortan at one third of Wobol, what is the total profit for SciTec products in June and July, assuming 4% of products are defective and must be refunded?

            A: £1,363k

            B: £1,361k

            C: £1,307k

            D: £1,311k

Written Solutions

Step 1: Calculate the selling price of Tortan so that we have all three sales prices.

\dfrac{1}{3}\text{ of Wobol }=\dfrac{1}{3} \times \pounds12 = \pounds4

Sales prices:

\text{Wobol: }\pounds12

\text{Muspril: }\pounds10

\text{Tortan: }\pounds4

Step 2: Identify sales figures of all products for June and July, then multiply by sales price.

\begin{aligned}\text{Wobol: }&(25,000+31,000) \times \pounds12 = \pounds672k \\ \text{Muspril: }&(26,000+29,000) \times \pounds10 = \pounds550k \\ \text{Tortan: }&(26,000 + 23,000) \times \pounds4 = \pounds196k \end{aligned}

Step 3: Since 4% of all products are defective we can subtract this percentage from the total sales of all three products. A 4$ decrease is equivalent to a multiplier of 0.96.

\pounds672k + \pounds550k + \pounds196k = \pounds 1,418k

0.96 \times \pounds1,418k \approx \bold{\pounds1,361k}

Question 7

Wobol sells at £600 per batch of 50. If the batch size increases in May by 22% while the selling price remains the same, what is the approximate difference in revenue generated by Wobol between April and May?

            A: £21,500

            B: £19,700

            C: £26,100

            D: £27,900

Written Solutions

Step 1: Calculate the revenue for Wobol in April given that it is sold in batches of 50 for £600 a batch.

22,000 \div 50 = 440 \text{ (number of batches)}

440 \times 600 = \pounds264,000 \text{ (revenue in April)}

Step 2: Calculate the revenue for Wobol in May give that the batch size has increase by 22% from April. An increase of 22% is a multiplier of 1.22.

1.22 \times 50 = 61 \text{ (new batch size)}

24,000 \div 61 = 393.44 \text{ (number of batches to 2d.p.)}

393 \times 600 = \pounds236,064 \text{ (revenue in May)}

Step 3: Find the difference in revenues between April and May and round.

\pounds264,000 - \pounds236,064 = \bold{\pounds27,900}

Question 8

Between June – August, how many times were products average sales per day greater than £1225, given that 8% of stock is sold for testing in July and must be excluded?

            A: 2 times

            B: 3 times

            C: 4 times

            D: 5 times

Written Solutions

Step 1: Calculate the average sales per day for each product in June by taking the sales figure and dividing by the number of days.

\begin{aligned}\text{June: Wobol: }&25,000 \div 21 = 1,190 \\ \text{Muspril: }&26,000 \div 21 = 1,238 \checkmark \\ \text{Tortan: }&26,000 \div 21 = 1,238 \checkmark \end{aligned}

Step 2: Calculate sales per day for July – these figures must be reduced by 8%, which is a multiplier of 0.92.

\begin{aligned}\text{July: Wobol: }&(31,000 \times 0.92) \div 22 = 1,296 \checkmark \\ \text{Muspril: }&(29,000 \times 0.92) \div 22 = 1,213 \\ \text{Tortan: }&(23,000 \times 0.92) \div 22 = 961 \end{aligned}

Step 3: Calculate the average sales per day for each product in August by taking the sales figure and dividing by the number of days.

\begin{aligned}\text{August: Wobol: }&27,000 \div 23 = 1,174 \\ \text{Muspril: }&24,000 \div 23 = 1,043 \\ \text{Tortan: }&20,000 \div 23 = 870 \end{aligned}

Finally, count up the occurrences of an averages sales per day greater than £1225 for a total of 3 times.

Question 9

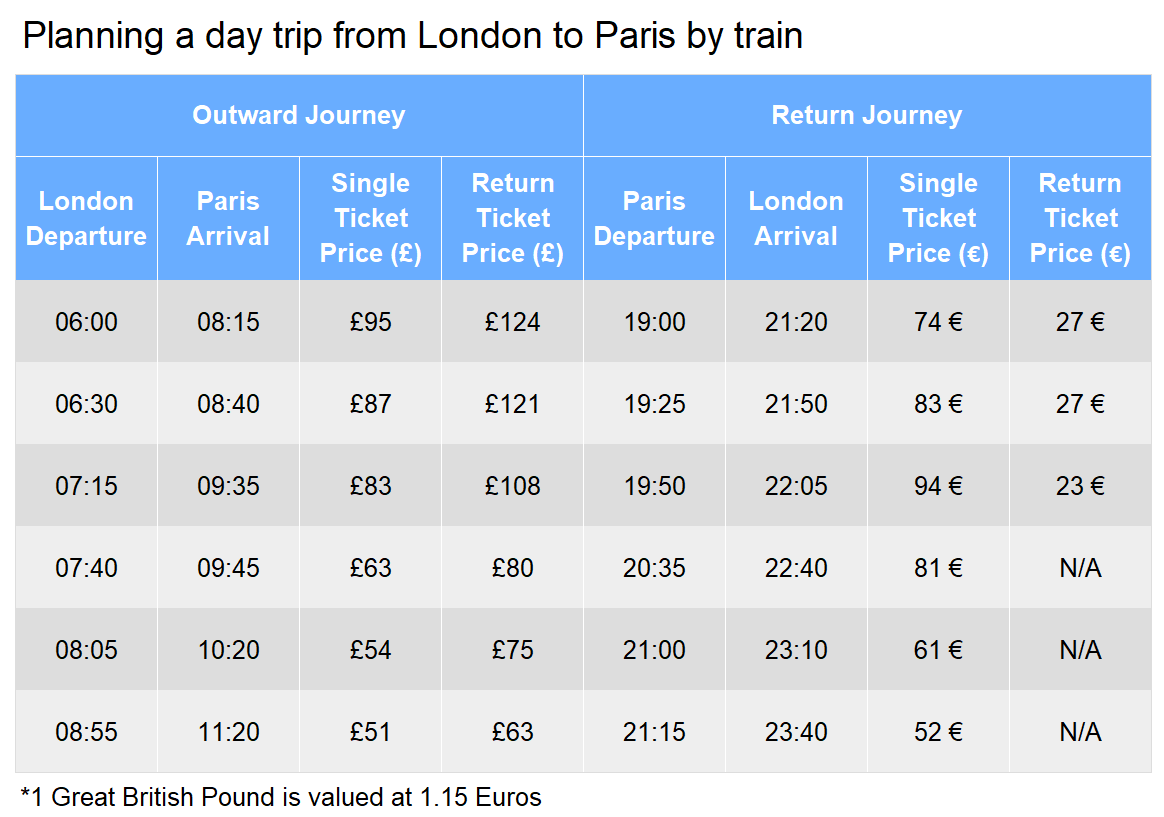
Based on the fastest and slowest trains from London to Paris or vice versa what is the maximum difference in average speed of the train? The distance travelled is 284 miles.

            A: 14.61mph

            B: 18.8mph

            C: 24.5mph

            D: 12.3mph

Written Solutions

Step 1: Identify the fastest and slowest trains by subtracting departure time from arrival time.

i.e. 08:15 - 06:00 = 02:15

The fastest train is the 07:40 departure from London with a duration of 2:05

The slowest train is the 08:55 departure from London with a duration of 2:25

Other trains also have the same journey speed as the above.

Step 2: Calculate the speed of the fastest train. We must first convert the 24-hour time into minutes (or fractions of hours).

\begin{aligned}02:05 &\equiv 125 \text{ minutes} \\ \text{speed} &= \dfrac{\text{distance}}{\text{time}} \\ \dfrac{284\text{ miles}}{125\text{ minutes}} &= 2.272\text{ miles per minute} \end{aligned}

Now convert back to miles per hour by multiplying by 60

2.272\text{ miles per minute} \times 60 \text{ minutes} = 136.32\text{mph}

Step 3: Calculate the speed of the slowest train in the same way

\begin{aligned}02:25 &\equiv 145 \text{ minutes} \\ \text{speed} &= \dfrac{\text{distance}}{\text{time}} \\ \dfrac{284\text{ miles}}{145\text{ minutes}} &= 21.96\text{ miles per minute} \end{aligned}

Now convert back to miles per hour by multiplying by 60

1.96\text{ miles per minute} \times 60 \text{ minutes} = 117.5\text{mph}

Step 4: Finally calculate the difference between the two speeds.

136.32\text{mph} - 117.5\text{mph} \approx \bold{18.8\text{mph}}

Question 10

A tourist has €200 for a day trip to Paris but cannot take a return journey as these have been booked. How much money in GBP does he have left when he returns to London if he takes the cheapest trains possible?

            A: £77.69

            B: £97.21

            C: £119.24

            D: £83.15

Written Solutions

Step 1: Locate the cheapest outward and return journeys.

Outward: 08:55 – 11:20 for £51

Return: 21:15 to 23:40 for €52

Step 2: Work through the journey, converting currency to calculate the remaining value.

Convert €200 into pounds – 200 \div 1.15 = \pounds173.91

Subtract the first journey – \pounds173.91 - \pounds51 = \pounds122.91

Convert the return journey into pounds 52 \div 1.15 = \pounds45.22

Subtract the return journey – \pounds122.91 - \pounds45.22 = \bold{\pounds77.69}

Question 11

A businessman leaves London on the 8:05 train, he plans to visit museums for 2.75 hours, attend a meeting for 90 minutes and will take two breaks of 20 minutes during the day. Assuming he has £61 to pay for his single ticket to return to London, and returns as early as possible, how much extra free time does he have while in Paris?

            A: 3:45

            B: 4:25

            C: 5:45

            D: 6:25

Written Solutions

Step 1: We need to add all these times to calculate the duration of his activities in Paris. First we need to convert all of them into hours and minutes.

\begin{aligned}2.75\text {hours} &= 2\text{ hours} 45\text{ minutes} \\ 90\text {minutes} &= 1\text{ hours} 30\text{ minutes} \\ 2 \times 20\text{ minutes} &= 40\text{ minutes}\end{aligned}

The train arrives in Paris at 10:20, now we add these times onto the arrival time, taking care to add hours and minutes separately.

\text{Hours: }10 + 2 + 1 = 13\text{ hours}

\text{Minutes: }20 + 45 + 30 + 40 = 135\text{ minutes}

Now convert the minutes back into hours and minute to calculate the time his activities end.

135\text{ minutes} = 2\text{ hours} 15\text{ minutes}

So, his activities end at 15:15.

Step 2: Convert the £61 to euros to compare it with ticket prices.

\pounds61 \times 1.15 = 70.15 \text{ euros}

So, the earliest train he can take home is at 21:00.

Step 3: Find the difference between 15:15 and 21:00 to calculate his free time.

21:00 - 15:15 = \bold{05:45}

Question 12

What is the average cost per hour of a return ticket from 19:00 onwards in pounds?

            A: £9.14

            B: £9.53

            C: £9.34

            D: £9.57

Written Solutions

Step 1: Calculate the total duration and cost of the three journeys with return tickets from 19:00 onwards.

02:20 + 02:25 + 02:15 = 6\text{ hours} 60\text{ minutes} = 7\text{ hours}

27 + 27 + 23 = 77\text{ euros}

Step 2: Calculate the cost per hour.

\dfrac{\text{Total cost}}{\text{Number of hours}} = \dfrac{77 \text{ euros}}{7} = 11\text{ euros per hour}

Step 3: Convert this into pounds. 1 pound is 1.15 euros so we must divide to convert from euros to pounds.

11\text{ euros} \div 1.15 = \bold{\pounds9.57}

Question 13

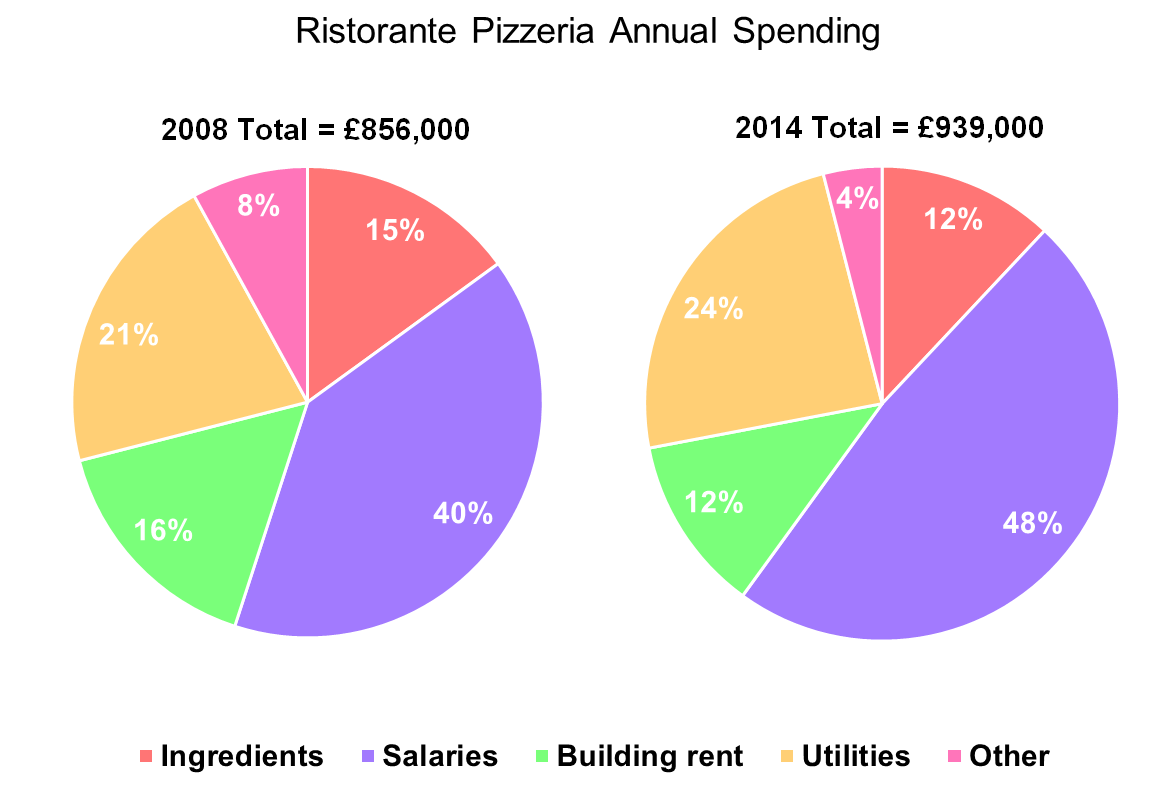
By 2014, the salary for the Head Chef was £65,000 per year, which is an increase of 25% on her salary for 2008. What proportion of the money spent on wages in 2008 was spent on the Head Chef’s salary?

                A: 12.8%

                B: 12.4%

                C: 16.1%

                D: 15.2%

Written Solutions

Step 1: Determine how much the Head Chef earned in 2008.

A 25% increase corresponds to a multiplier of 1.25. This mean, her 2008 salary multiplied by 1.25 must be equal to 65,000. So, to find her 2008 wages we must divide 65,000 by 1.25.

\text{2008 salary } = 65,000 \div 1.25 = \pounds 52,000

Step 2: Find the amount of money spent on wages in 2008.

\text{Money spent on salaries } = 40\% \text{ of } 856,000 = 0.4 \times 856,000 = \pounds 342,400

Step 3: Calculate the percentage of £342,400 which constitutes the Head Chef’s salary.

\dfrac{52,000}{342,400} \times 100 = 15.2\%

Question 14

The spending on utilities is broken up into water, gas, and electricity. The ratio of spending on water to gas to electricity is 1: 5: 4 in 2008, and 2: 8: 9 in 2014. Calculate the increase in the cost of the electricity bill from 2008 to 2014.

                A: £31,007.62

                B: £34,845.47

                C: £22,125.02

                D: £25,902.98

Written Solutions

Step 1: Calculate the spending on electricity in 2008.

Firstly, calculate the money spent on utilities in 2008.

21\% \text{ of } 856,000 = 0.21 \times 856,000 = \pounds 179,760.

The ratio of water to gas to electricity is 1:5:4, so the fraction of money spent on electricity in 2008 is \frac{4}{1 + 5 + 4} = \frac{2}{5}. Therefore,

\text{2008 electricity cost } = \dfrac{2}{5} \times 179,760 = \pounds 71,904

Step 2: Calculate the spending on electricity in 2014.

Firstly, calculate the money spent on utilities in 2014.

24\% \text{ of } 939,000 = 0.24 \times 939,000 = \pounds 225,360

The ratio of water to gas to electricity is 2:8:9, so the fraction of money spent on electricity in 2014 is \frac{9}{2 + 8 + 9} = \frac{9}{19}. Therefore,

\text{2014 electricity cost } = \dfrac{9}{19} \times 225,360 = \pounds 106,749.47

Step 3: Determine the increase.

106,749.47 - 71,904 = \pounds34,845.47.

Question 15

The spending for 2015 will increase to £951,000 in 2015, partly because of a 5% increase in the cost of building rent on the year before. In 2015, what will be the ratio of spending on building rent to spending on ingredients, assuming the money spent on ingredients constitutes the same percentage of the total as the previous year?

                A: 1.03 : 1

                B: 1.06 : 1

                C: 1.02 : 1

                D: 1.04 : 1

Written Solutions

Step 1: Calculate the cost of rent in 2015.

A 5% increase corresponds to the multiplier 1.05. So, we get:

12 \% \text{ of } 939,000 = 0.12 \times 939,000 = \pounds 112,680

\text{Then, a 5\% increase } = 1.05 \times 112,680 = \pounds 118,314

Step 2: Calculate the money spent on ingredients in 2015.

\text{2015 spend on ingredients } = 0.12 \times 951,000 = \pounds 114,120

Step 3: Form the ratio and simplify it by dividing through by the smaller value.

\begin{aligned}\text{building rent : ingredients} &= 118,314 : 114,120 \\ &= \dfrac{118,314}{114,120} : \dfrac{114,120}{114,120} \\ &= 1.04 : 1 \end{aligned}

Question 16

In 2008, £1 of ingredients sold for an average of £6.90 once cooked. In 2014, this value was £8.91. Given that freezer malfunctions resulted in £3,600 worth of food being discarded in 2014, what is the percentage change in sales of food between 2008 and 2014?

                A: 12.7%

                B: 9.7%

                C: 5.5%

                D: 10.0%

Written Solutions

Step 1: Determine how much money was spent on ingredients in 2008 and 2014.

\text{2008 ingredients cost } = 15\% \text{ of } 856,000 = 0.15 \times 856,000 = \pounds 128,400

\text{2014 ingredients cost } = 12\% \text{ of } 939,000 = 0.12 \times 939,000 = \pounds 112,680

Step 2: Calculate the sales of food in 2008 and 2014, remembering to remove the money spent on discarded food.

\text{2008 sales } = 128,400 \times 6.90 = \pounds 885,960

\begin{aligned}&\text{Money spent on usable food in 2014 } = 112,680 - 3,600 = \pounds 109,080 \\ &\text{So, 2014 sales } = 109,080 \times 8.91 = \pounds 971,902.80\end{aligned}

Step 3: Work out the percentage change.

\dfrac{971,902.80 - 885,960}{885,960} \times 100 = 9.7 \%

Question 17

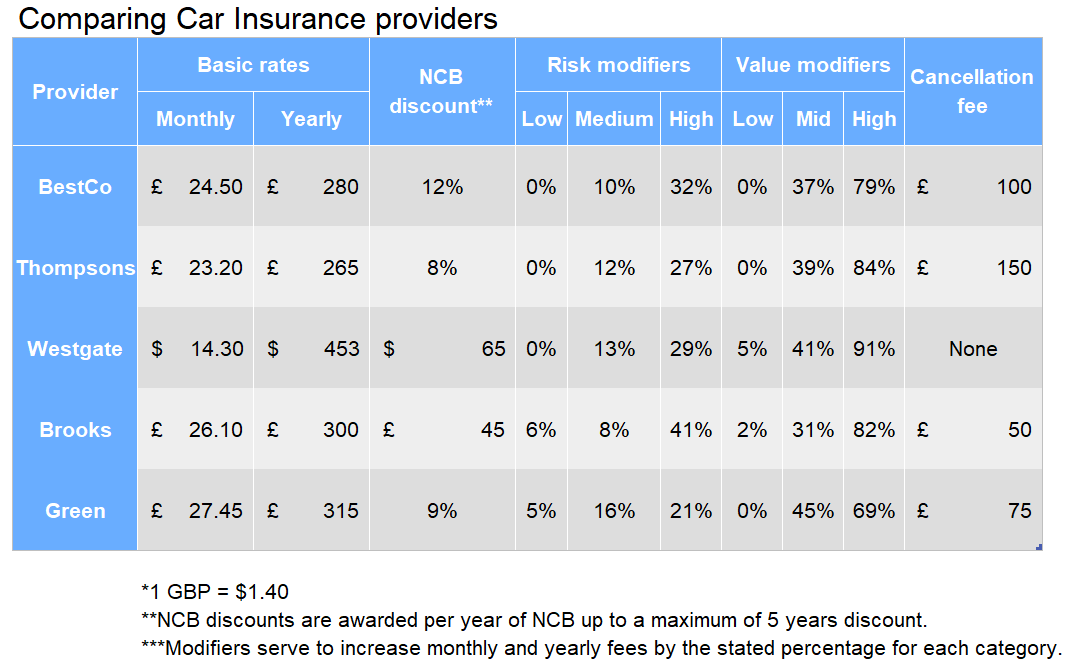
What is the ratio of the yearly cost of a high value car in a medium risk area with two years of NCB discount between BestCo and Thompsons?

                A: 1: 1.06

                B: 1: 1.07

                C: 1: 1.08

                D: 1: 1.09

Written Solutions

Step 1: Calculate the cost for BestCo. We need to increase by 10% for a medium risk area and 79% for a high value car which correspond to multipliers of 1.10 and 1.79 respectively. We also need to apply two decreases of 12%, which corresponding to a multiplier of 0.88 \times 0.88\text{ or }0.88^2

\pounds280 \times 1.1 \times 1.79 \times 0.88^2 = \pounds426.94

Step 2: Similarly calculate this for Thompsons, the multipliers change to 1.12, 1.84 and 0.92^2 respectively.

\pounds265 \times 1.12 \times 1.84 \times0.92^2 = \pounds462.23

Step 3: Now form the ratio and simplify.

\begin{aligned}\text{BestCo}&:\text{Thompsons} \\ \pounds426.94 &: \pounds462.23 \\ \dfrac{426.94}{426.94}&:\dfrac{462.23}{426.94} \\ 1&:1.08\end{aligned}

Question 18

What is the difference in price (to the nearest 10p) between Westgate and Brooks, in pounds, of a monthly contract with 1 years NCB, for a mid-value car in a low risk area.

                A: £10.50

                B: £11.90

                C: £11.00

                D: £12.30

Written Solutions

Step 1: Calculate the price of Westgate. Since NCB is awarded per year we need to divide that discount by 12 – since it is a flat amount this is acceptable. The low risk modifier does not change the price, and the value modifier is an increase of 41% or a multiplier of 1.41

(\$24.30 * 1.41) - (\$65 \div 12) = \$28.85

Step 2: It is a similar process for Brooks, in this case we have a low risk modifier of 6% (multiplier of 1.06) and a mid-value modifier of 31% (multiplier of 1.31)

(\pounds26.10 \times1.06 \times1.31) - (\pounds45 \div 12) = \pounds32.49

Step 3: Before we calculate the difference, we need to convert dollars into pounds. The exchange rate is given, and we must divide the value for Westgate by 1.40 to convert into pounds.

\$28.85 \div 1.40 = \pounds20.61

\pounds32.49 - \pounds20.61 \approx \bold{\pounds11.90}

Question 19

A customer with Green wants to cancel their yearly contract and swap to BestCo. They have 3 years NCB, live in a low risk area and have a low value vehicle. Over the next year, how much money do they gain or lose by making this change to the nearest pound?

                A: £18 gain

                B: £21 loss

                C: £12 gain

                D: £17 loss

Written Solutions

Step 1: We need the yearly cost of both insurance providers, starting with Green. A low risk area means a 5% increase, and three years of NCB is a 9% reduction three times, or a multiplier of 0.91^3

\pounds315 \times0.91^3 \times 1.05 \approx \pounds249

Step 2: Calculate the yearly cost of BestCo, making sure to add the cost of cancelling the Green contract. There are no modifiers for risk or value, and the 12% NCB reduction occurs three times for a multiplier of 0.88^3

(\pounds280 \times 0.88^3) + \pounds75 = \pounds266

This adds up to a loss of £17 over the year.

Question 20

A customer of Greens, who has 5 years NCB, lives in a low risk area with a high value car is looking to downgrade to a mid-value car. What is the approximate yearly saving if they also change from their current monthly policy to one that is paid yearly?

                A: £65.50

                B: £71.30

                C: £74.70

                D: £56.20

Written Solutions

Step 1: Calculate the current cost of the monthly contract, spread across one year. Multiply the monthly price by 12 and then make the following modifications: 5 years NCB is a reduction of 9% for each year so a multiplier of 0.91^5, low risk means a 5% increase which is a multiplier of 1.05, and finally a high value car is a 69% increase or a multiplier of 1.69.

\pounds27.45 \times 12 \times 0.91^5 \times 1.05 \times 1.69 =\pounds364.76

Step 2: Calculate the change form monthly to yearly payments and mid value car (multiplier is now 45% or 1.45.

\pounds315 \times 0.91^5 \times 1.05 \times 1.45 = \pounds299.28

Step 3: The yearly saving is approximately £65.50