Question 1

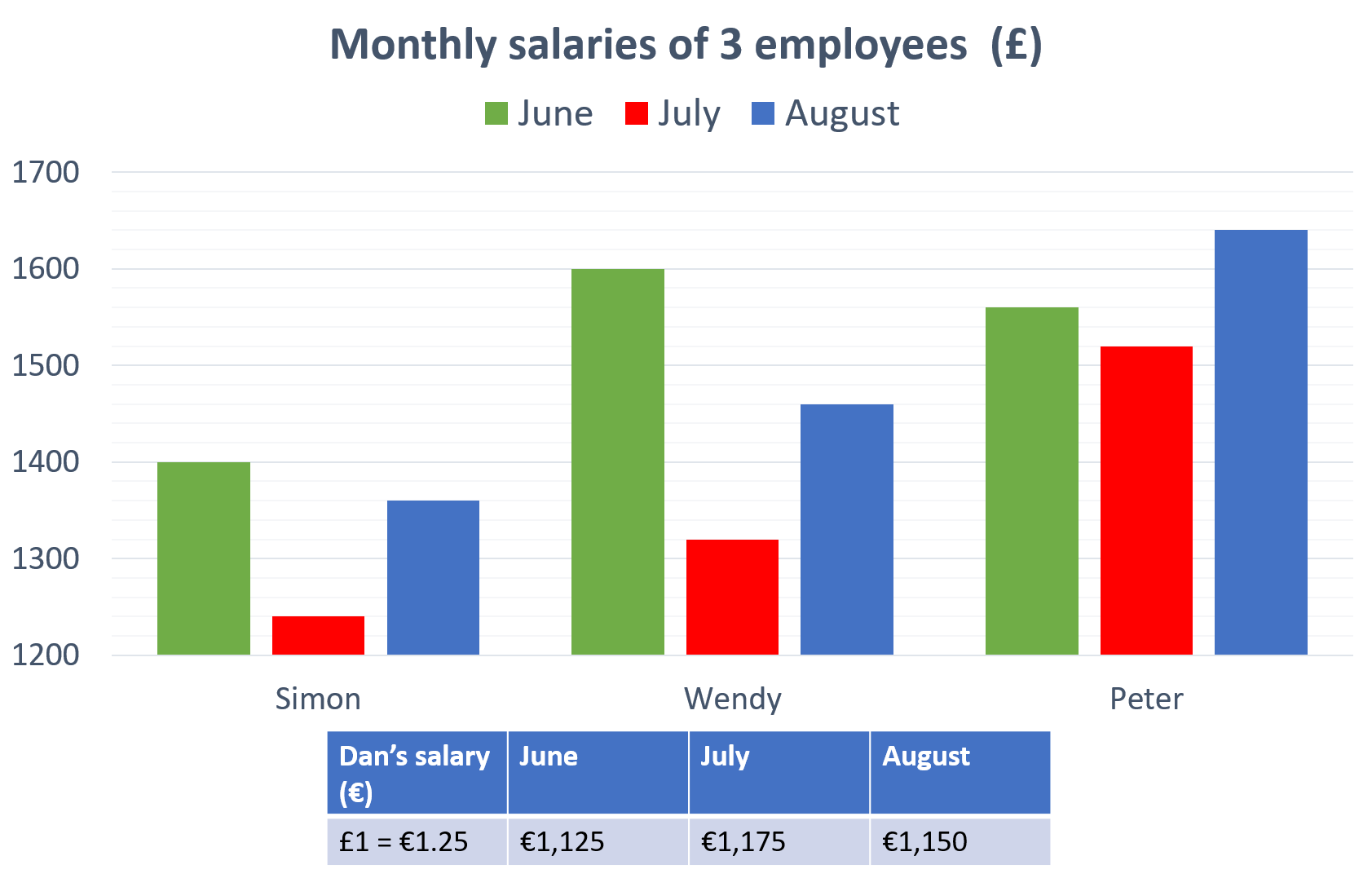
What was the percentage decrease (correct to 1 decimal place) in total salary for Simon and Peter combined from June to July?

A: 6.8%

B: 9.2%

C: 12.7%

D: 17.1%

Written Solutions

In June, Simon and Peter’s combined salary was \pounds1400 + \pounds1560 = \pounds2960.

In July, Simon and Peter’s combined salary was \pounds1240 + \pounds1520 = \pounds2760

As a percentage decrease, this can be calculated as follows:

\dfrac{\pounds2960 - \pounds2760}{\pounds2960} \times100 = 6.8\% correct to one decimal place.

Question 2

What is Wendy’s take home pay in June if she is taxed at 20% on everything she earns above £950?

A: £1128

B: £1150

C: £1356

D: £1470

Written Solutions

Wendy’s salary in June is \pounds1600. If she is taxed at 20\% on her salary above \pounds950, then we need to work out her taxable income:

\pounds1600 - \pounds950 = \pounds650 taxable income.

If she is taxed at 20\% on this, then the amount she pays in tax can be calculated as follows:

\pounds650 \times0.2 = \pounds130.

Therefore if she pays \pounds130 tax from her \pounds1600 salary, then she is paid a total of \pounds1600 - \pounds130 = \pounds1470

Question 3

As a percentage to the nearest whole number, how much less was Dan paid between June and August than Peter?

A: 28%

B: 29%

C: 42%

D: 53%

Written Solutions

Between June and August, Dan is paid €1125 + €1175 + €1150 = €3450

In pounds, this can be calculated as follows:

€3450 \div €1.25 = \pounds2760

Between June and August, Peter is paid \pounds1560 + \pounds1520 + \pounds1640 = \pounds4720

If Dan is paid \pounds2760 and Peter is paid \pounds4720, this is a difference of \pounds4720 - \pounds2760 = \pounds1960.

\pounds1960 as a percentage of Peter’s pay of \pounds4720 is:

\dfrac{\pounds1960}{\pounds4720} \times100 = 41.5\% or 42\% to the nearest whole number.

Question 4

Peter needs to repay £180 per month from his pre-tax salary for a bike and is then taxed at 20% on everything above £950 per month.  If he pays £400 per month for rent and bills, how much does he spend on food in this 3 month period if he spends 35% of his remaining salary on food?

A: £627.84

B: £680.45

C: £790.95

D: £949.90

Written Solutions

Peter’s salary for the period June – August is \pounds1560 + \pounds1520 + \pounds1640 = \pounds4720. Before he is taxed \pounds180 per month is deducted. Since this is a period of 3 months, we need to deduct 3\times\pounds180 = \pounds540 from his pre-tax salary.

\pounds4720 - \pounds540 = \pounds4180

If Peter is taxed on everything above \pounds950 per month, then we can work out his taxable income by simply subtracting \pounds950\times3 = \pounds2850 from the \pounds4180:

\pounds4180 - \pounds2850 = \pounds1330

If he is taxed at 20\% on \pounds1330, then he will pay 0.2\times\pounds1330 = \pounds266 in tax.
Therefore his pay for the three month period is:

\pounds4180 - \pounds266 = \pounds3914

We also need to deduct three month’s worth of rent and bills which is 3\times\pounds400 = \pounds1200:

\pounds3914 - \pounds1200 = \pounds2714

If he spends 35\% of his salary on food, then we can calculate exactly how much he spends on food over the three month period:

\pounds2714\times0.35 = \pounds949.90

This is quite a long question but, by not deleting answers in your calculator, you will save time by not having to re-enter the starting number in every calculation.

Question 5

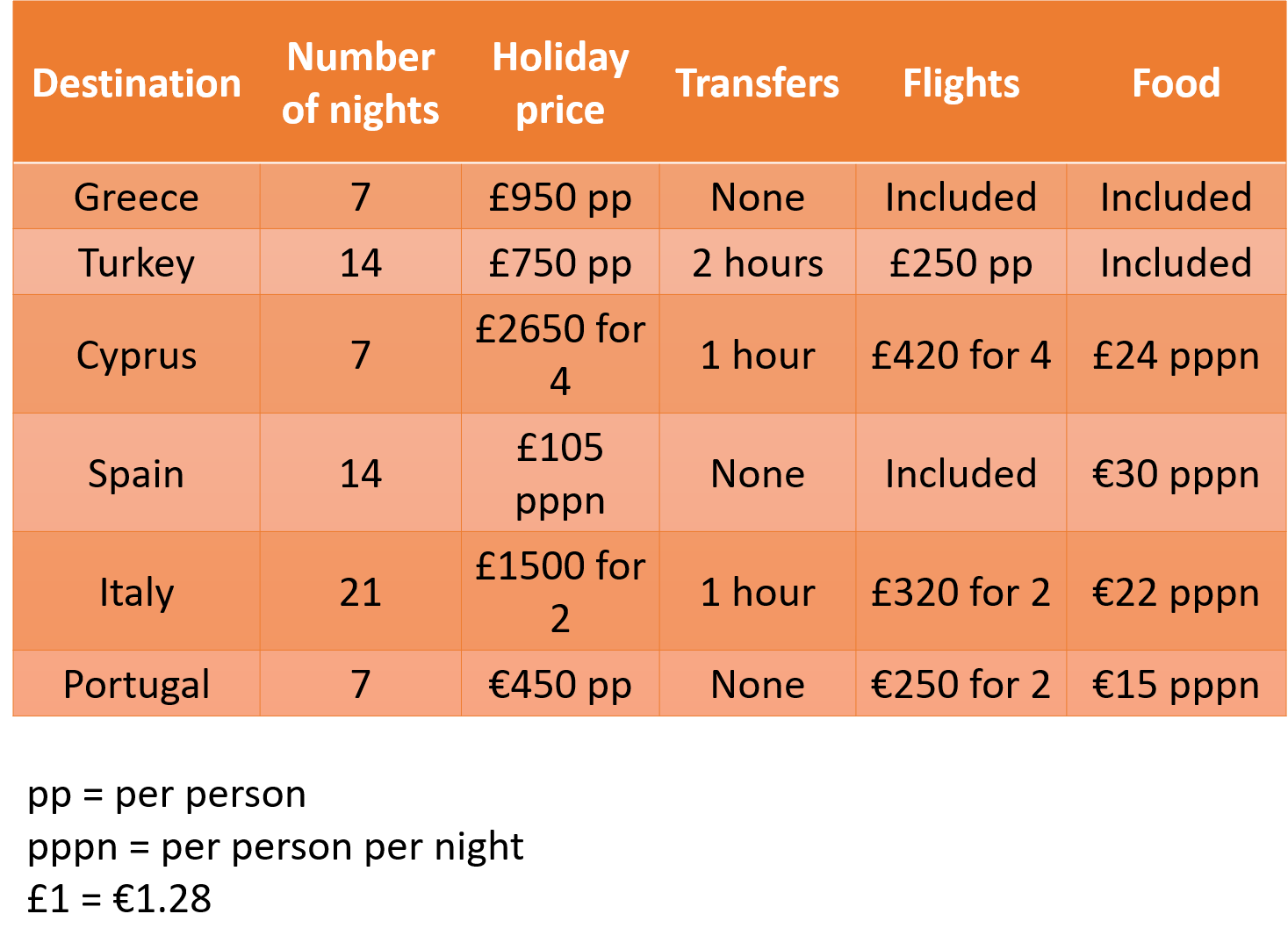
The stated price of a holiday to Cyprus increases by 27%.  What is the overall percentage increase of the holiday for a family of four, factoring in the costs of flights and food?

A: 16%

B: 19%

C: 23%

D: 27%

Written Solutions

The stated holiday price to Cyprus is \pounds2640. If this increases by 27\%, then its new price will be:

\pounds2650\times1.27 = \pounds3365.50

If we add in the costs of flights and food on top of this increases price, we can determine how much the overall holiday costs.

\pounds3365.50 + \pounds420 + (\pounds24\times7\times4) = \pounds4457.50

The original holiday would have cost:

\pounds2650 + \pounds420 + (\pounds24\times7\times4) = \pounds3742

The percentage increase in the cost of the holiday can be calculated as follows:

\dfrac {\pounds4457.50 - \pounds3742}{\pounds3742} \times100 = 19.12\% or 19\% to the nearest whole number.

Question 6

Two people split the holiday price of a holiday to Portugal in the ratio of 2 : 3.  All other costs are shared evenly.  What is the overall ratio of cost between the two people?

A: 3 : 7

B: 8 : 11

C: 77 : 59

D: 103 : 121

Written Solutions

The holiday price for a holiday for two people to Portugal is €450\times2 = €900.

If this is split in the ratio of 2 : 3, then that means that one person will pay \frac{2}{5} of the amount and the other will pay \frac{3}{5}. (We are dealing with fifths because 2 + 3 = 5)

Therefore the person paying \frac{2}{5} will pay:

€900\times \frac{2}{5} = €360

The other person will pay €900 - €360 = €540

Flights cost €250 for 2 people. If this cost is shared evenly, then each person will pay €125.

Meals are €15 per person per night, so for a week, food will cost €15\times7 = €105.

In total, one person will pay €105 + €125 + €360 = €590

The other person will pay €105 + €125 + €540 = €770

Therefore the ratio of what they pay is 770 : 590 which can easily be simplified to 77 : 59.

Question 7

The Portugal deal is amended at the last minute.  The holiday price is reduced by 15%, the flight cost remains the same and the food is included for free.  How much savings can be made to the nearest pound for a holiday for 4 people for 7 nights?

A: £490

B: £539

C: £690

D: £820

Written Solutions

If the Portugal price has been reduced by 15\%, then the new holiday price can be calculated as follows:

€450\times0.85 = €382.50

This is a saving of €450 - €382.50 = €67.50 per person.

If there are four people going on holiday, then this is a saving of €67.50\times4 = €270.

If the food is free, then this is another saving:

€15\times7\times4 = €420

Therefore the total savings come to a total of €420 + €270 = €690

All we need to do now is to convert this to pounds:

€690 \div €1.28 = \pounds539 to the nearest pound.

Question 8

A couple book a holiday to Italy and share the overall cost.  How much does the holiday cost them each to the nearest pound?

A: £956

B: £1064

C: £1030

D: £1271

Written Solutions

The only thing which makes this question complicated is that the food is in euros.

The total cost of the food is €22\times2\times21 = €924

Now we need to convert the €924 into pounds:

€924 \div €1.28 = \pounds721.88

For 2 people, the holiday costs \pounds1500 + \pounds320 + \pounds721.88 = \pounds2541.88, so will therefore cost half this amount per person, so the final answer is \pounds1271 to the nearest pound.

Question 9

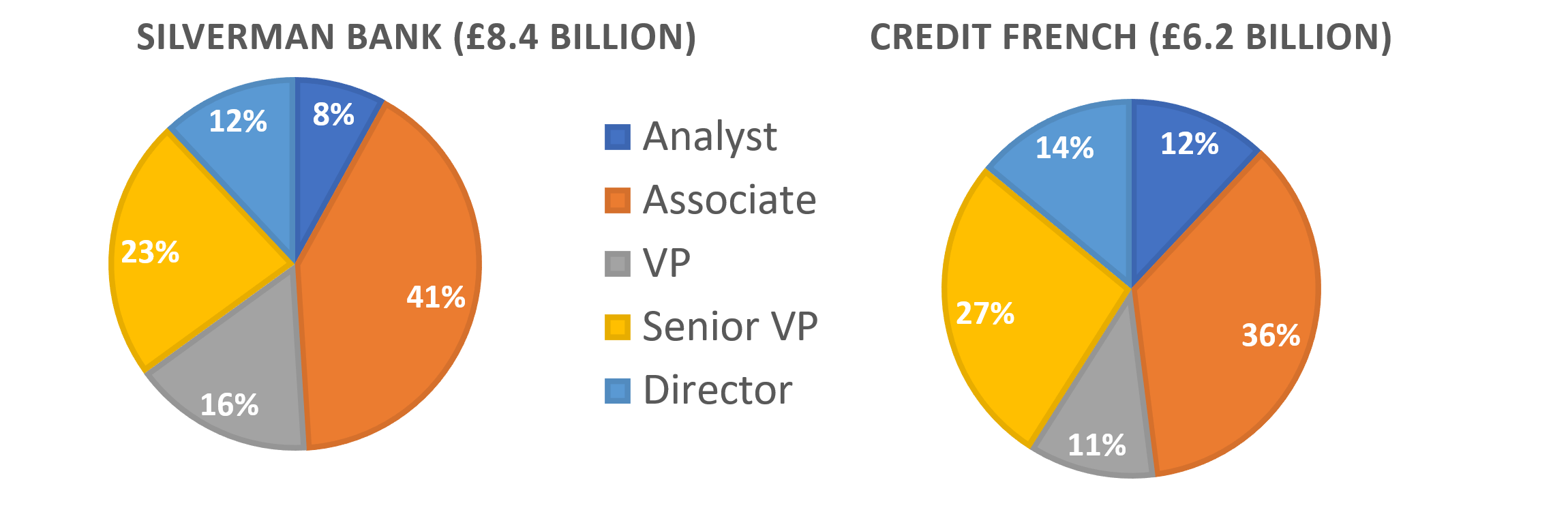
To the nearest pound, what is the difference between the annual wages of a VP in the two banks if there are 2500 VPs in Silverman Bank and 2038 in Credit French?

A: £16,786

B: £29,987

C: £143,784

D: £202,958

Written Solutions

At Silverman Bank, VPs comprise 16\% of the staff. If the total cost of Silverman’s staff is \pounds8.4 billion, then the amount assigned to VPs is:

\pounds8.4 billion\times 0.16 = \pounds1.344 billion

If there are 2500 VPs at Silverman’s bank, then we can calculate the wages of one VP as follows:

\pounds1.344 billion \div 2500 = \pounds537,600

At Credit French, VPs comprise 11\% of the staff. If the total cost of Silverman’s staff is \pounds 6.2 million, then the amount assigned to VPs is:

\pounds6.2 billion \times0.11 = \pounds0.682 billion

If there are 2038 VPs at Silverman’s bank, then we can calculate the wages of one VP as follows:

\pounds0.682 billion \div 2038 = \pounds334,641.81

The difference in pay between VPs at the two banks is \pounds537,600 - \pounds334,641.81 = \pounds202,958 to the nearest pound.

Question 10

What is the ratio of spending of wages on analysts for Silverman Bank and Credit French?

A: 3: 5

B: 6: 7

C: 28: 31

D: 43: 49

Written Solutions

Analysts comprised 8\% of Silverman. If the total cost of Silverman’s staff is \pounds8.4 billion, then the amount assigned to analysts is:

\pounds8.4 billion \times 0.08 = \pounds0.672 billion

Analysts comprised 12\% of Credit French. If the total cost of Credit French’s staff is \pounds6.2 billion, then the amount assigned to analysts is:

\pounds6.2 billion \times 0.12 = \pounds0.744 billion

The ratio of spending is \pounds0.672 billion : \pounds0.744 billion. We can simplify this ratio with minimal effort to 672 : 744.

\dfrac{672}{744} = \dfrac {28}{31}

If you type 672 \div 744 into your calculator, your calculator may even give you the answer of \dfrac {28}{31}, otherwise you will need to simplify the fraction \dfrac{672}{744} until you eventually reach of \dfrac {28}{31}

Question 11

Silverman want to decrease spending on directors to 10% of overall wages.  Assuming that overall staffing costs will remain the same, how many directors do they need to make redundant if they are paid £1,425,000 each?

A: 85

B: 96

C: 102

D: 118

Written Solutions

Silverman’s spending on directors is currently 12\%. 12\% of the total staffing costs of \pounds8.4 billion can be calculated as follows:

0.12\times\pounds8.4 billion = \pounds1.008 billion.

If Silverman want to reduce this figure to 10\% and keep overall staffing costs the same, then directors will cost a total of:

0.1 \times \pounds8.4 billion = \pounds0.84 billion

This means that they will have saved a total of \pounds1.008 billion - \pounds0.84 billion = \pounds0.168 billion. At this stage it might be worth converting \pounds0.168 billion to \pounds168,000,000

If each director costs the firm \pounds1,425,000 , we can calculate the number of directors they need to get rid of as follows:

\pounds168,000,000 \div \pounds1,425,000 = 117.89 directors.

Since it is not possible to make 117.89 directors redundant to meet this cost saving, they will need to make 118 redundant.

Question 12

If Credit French promote half of their analysts to associates, how much do associates earn if, following this promotion, there are now 34,720 associates?

A: £63,000

B: £75,000

C: £83,000

D: £102,000

Written Solutions

Analysts comprise 12\% of the work force at Credit French. If half of them are promoted to associates, then this means that 6\% of the overall workforce are promoted so the overall percentage of associates will move from 36\% to 42\%.

If the staffing costs are \pounds6.2 billion and 42\% are associates, then this means that the overall cost of associates is:

\pounds6.2 billion \times 0.42 = \pounds2.604 billion

If this represents 34,720 associates, then we can now calculate how much one associate earns:

\pounds2.604 billion \div 34,720 = \pounds75,000

(This answer is probably easier to calculate if you convert \pounds2.604 billion to \pounds2,604,000,000 first or simply multiply your answer by a billion (1,000,000,000).)

Question 13

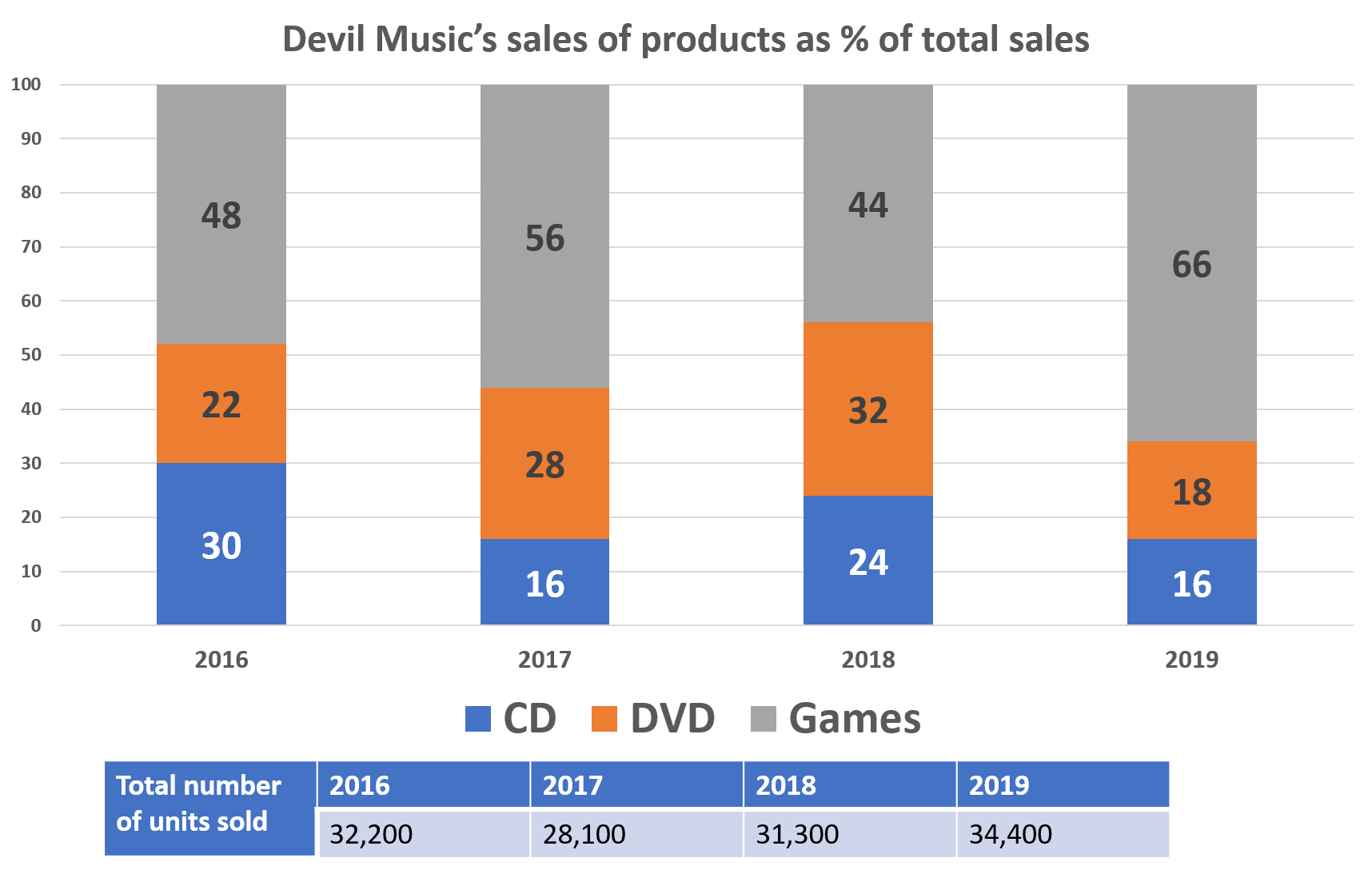
Over the 4 year period, sales of DVDs are split between kids DVDs and adult DVDs in the ratio of 1 : 3.  How many adult DVDs were sold in total?

A: 7790

B: 9320

C: 16,840

D: 23,370

Written Solutions

In 2016, DVDs comprised 22\% of overall sales. If there were 32,200 sales in total, then we can calculate the number of DVD sales as follows:

32,200\times0.22 = 7084

In 2017, DVDs comprised 28\% of overall sales. If there were 28,100 sales in total, then we can calculate the number of DVD sales as follows:

28,100\times0.28 = 7868

In 2018, DVDs comprised 32\% of overall sales. If there were 31,300 sales in total, then we can calculate the number of DVD sales as follows:

31,300\times0.32 = 10,016

In 2019, DVDs comprised 18\% of overall sales. If there were 34,400 sales in total, then we can calculate the number of DVD sales as follows:

34,400\times0.18 = 6192

Therefore in total there were 7084 + 7868 + 10,016 + 6192 = 31,160 DVD sales.

If this was split in the ratio of 1 : 3, then this means that adult DVDs accounted for \frac{3}{4} of overall sales (we are dealing in quarters because 1 + 3 = 4).

31,160\times\frac{3}{4} = 23,370

Question 14

CDs sold for an average of £6.92, £7.12 and £6.86 in 2017, 2018 and 2019 respectively.  How much profit was made on CD sales if the total cost of buying the CDs was £55,000?

A: £37,757.44

B: £53,485.44

C: £67,355.20

D: £122,355.20

Written Solutions

First of all, we need to work out how many CDs were sold in each year.

In 2017, CD sales were 16\% of overall sales, so the number of CD sales was 0.16\times 28,100 = 4496. At an average selling price of \pounds6.92, the total of CD sales is:

\pounds6.92\times4496 = \pounds31,112.32

In 2018, CD sales were 24\% of overall sales, so the number of CD sales was 0.24\times31,300 = 7512. At an average selling price of \pounds7.12, the total of CD sales is:

\pounds7.12 \times 7512 = \pounds53,485.44

In 2019, CD sales were 16\% of overall sales, so the number of CD sales was 0.16\times34,400 = 5504. At an average selling price of\pounds6.86, the total of CD sales is:

\pounds6.86\times5504 = \pounds37,757.44

The total CD sales for this 3 year period came to:

\pounds31,112.32 + \pounds53,485.44 + \pounds37,757.44 = \pounds122,355.20. If you deduct the cost of buying the CDs, the overall profit was:

\pounds122,355.20 - \pounds55,000 = \pounds67,355.20

Question 15

In 2016, the average profit made on a game was £13.15.  56% of the overall profit in 2016 was from sales of games.  How much profit was made for CDs, DVDs and games combined in 2016?

A: £71,136.24

B: £135,879.86

C: £362,940

D: £687,995.72

Written Solutions

First of all, we can work out how many games were sold. Games were 48\% of the overall 32,200 units, so:

0.48 \times 32,200 = 15,456 games sold.

If the average profit was \pounds13.15 per game, then the total profit would be:

\pounds13.15\times15,456 = \pounds203,246.40

If \pounds203,246.40 represents 56\%

then:

1\% = \pounds203,246.40 \div 56 = \pounds3629.40

so:

100\% = \pounds3629.40\times100 = \pounds362,940

Question 16

In 2020, Devil Music expect sales to increase by the same percentage as the percentage increase in sales (rounded to the nearest percentage point) from 2018 to 2019.  If sales of games increase from 66% to 75% of overall sales, and profit of £16.45 is made on each game sold, how much profit will Devil Music make on games in 2020?

A: £146,985

B: £285,936

C: £466,851

D: £563,962

Written Solutions

Sales increased from 31,300 to 34,400. As a percentage, this can be calculated as:

\dfrac{34,400 - 31,300}{31,300} \times100 = 9.9\% (rounded to 10\%)

Therefore sales have increased by 10\%.

If sales again increase by 10\% from 2019 – 2020, then the number of units sold in 2020 is:

34,400\times1.1 = 37,840

If 75\% of sales is made from games, then we can calculate the number of games sold:

37,840\times0.75 = 28,380

If the company makes \pounds16.45 per game, then they will make \pounds16.45\times28,380 = \pounds466,851 profit in total.

Question 17

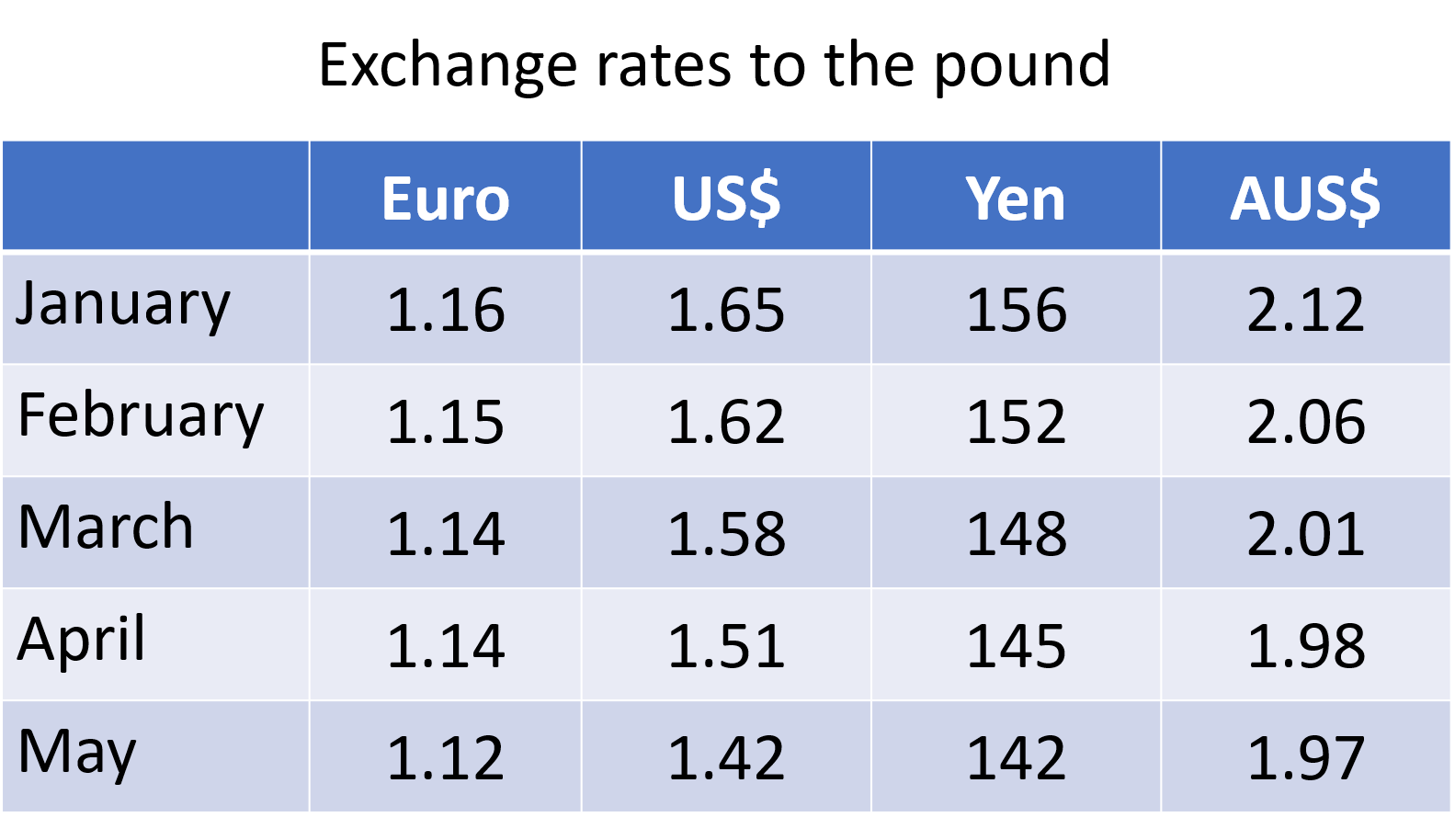
What is the value of 1 Australian dollar in euros in May?

A: €0.32

B: €0.45

C: €0.50

D: €0.57

Written Solutions

First of all, we can calculate what 1\text{A}\$ is worth in pounds:

1\text{A}\$ \div 1.97\text{A}\$ = \pounds0.5076

Now we can convert the pound value to euros:

\pounds0.5076 is worth \pounds0.5076\times €1.12 = €0.57

Question 18

A businessman buys £5,000 of euros in January which he then trades back to euros in February.  What profit has he made to the nearest pound?

A: £32

B: £43

C: £68

D: £124

Written Solutions

If the businessman exchanges \pounds5,000 into euros in January, we need to calculate how many euros he receives:

\pounds5,000 \times €1.16 = €5,800

If he trades these back into euros in February, he will receive:

€5,800 \div €1.15 = \pounds5043 (to the nearest pound).

Therefore, the businessman has made a profit of \pounds43.

Question 19

If the value of the Yen continues to fall at the same rate per month as the mean percentage per month between January and May (correct to 2 decimal places), what will the Yen be worth in June?  Give your answer to the nearest Yen.

A: 137 Yen

B: 138 Yen

C: 139 Yen

D: 140 Yen

Written Solutions

First of all, we need to work out the percentage decrease in the value of the Yen month by month.

From January to February, the percentage decrease was \dfrac{156 – 152}{156} = 2.56\% decrease (correct to 2 decimal places)

From February to March, the percentage decrease was \dfrac{152 – 148}{152} = 2.63\% decrease (correct to 2 decimal places)

From March to April, the percentage decrease was \dfrac{148 – 145}{148} = 2.03\% decrease (correct to 2 decimal places)

From April to May, the percentage decrease was \dfrac{145 – 142}{145} = 2.07\% decrease (correct to 2 decimal places)

Therefore, the mean percentage decrease was \dfrac{2.56 + 2.63 + 2.03 + 2.07}{4} = 2.32\%

Therefore, if the Yen falls by 2.32\% from May to June, the Yen will be worth:

142\times0.9768 = 138.7056 Yen or 139 to the nearest Yen

Question 20

A traveller converts £2,500 into Yen and £2,500 into Australian dollars in March before going on holiday.  If he spends 85% of the Yen and 78% of the Australian dollars, what is the difference (to the nearest pound) between the value of the remaining Yen and Australian dollars when he converts them back to pounds in May?

A: £86

B: £158

C: £170

D: £306

Written Solutions

First of all, we need to convert \pounds2,500 into Yen and \pounds2,500 into Australian dollars.

\pounds2,500\times148 Yen = 370,000 Yen

\pounds2,500\times \text{ A}\$2.01 = \text{ A}\$5,025

If he spends 85\% of the Yen, then he has 15\% remaining.

0.15\times370,000 Yen = 55,500 Yen remaining

55,500 Yen in pounds is:

55,500 Yen \div 142 Yen = \pounds390.85

If he spends 78\% of the Australian dollars, he has 22\% remaining.

0.22 \times \text{ A}\$5,025 = \text{ A}\$1105.50

A$1105.50 in pounds is:

\text{ A}\$1105.50 \div \text{ A}\$1.97 = \pounds561.16

The difference between the values of the remaining currency is:

\pounds561.16 - \pounds390.85 = \pounds170.31 or \pounds170 to the nearest pound.