Question 1

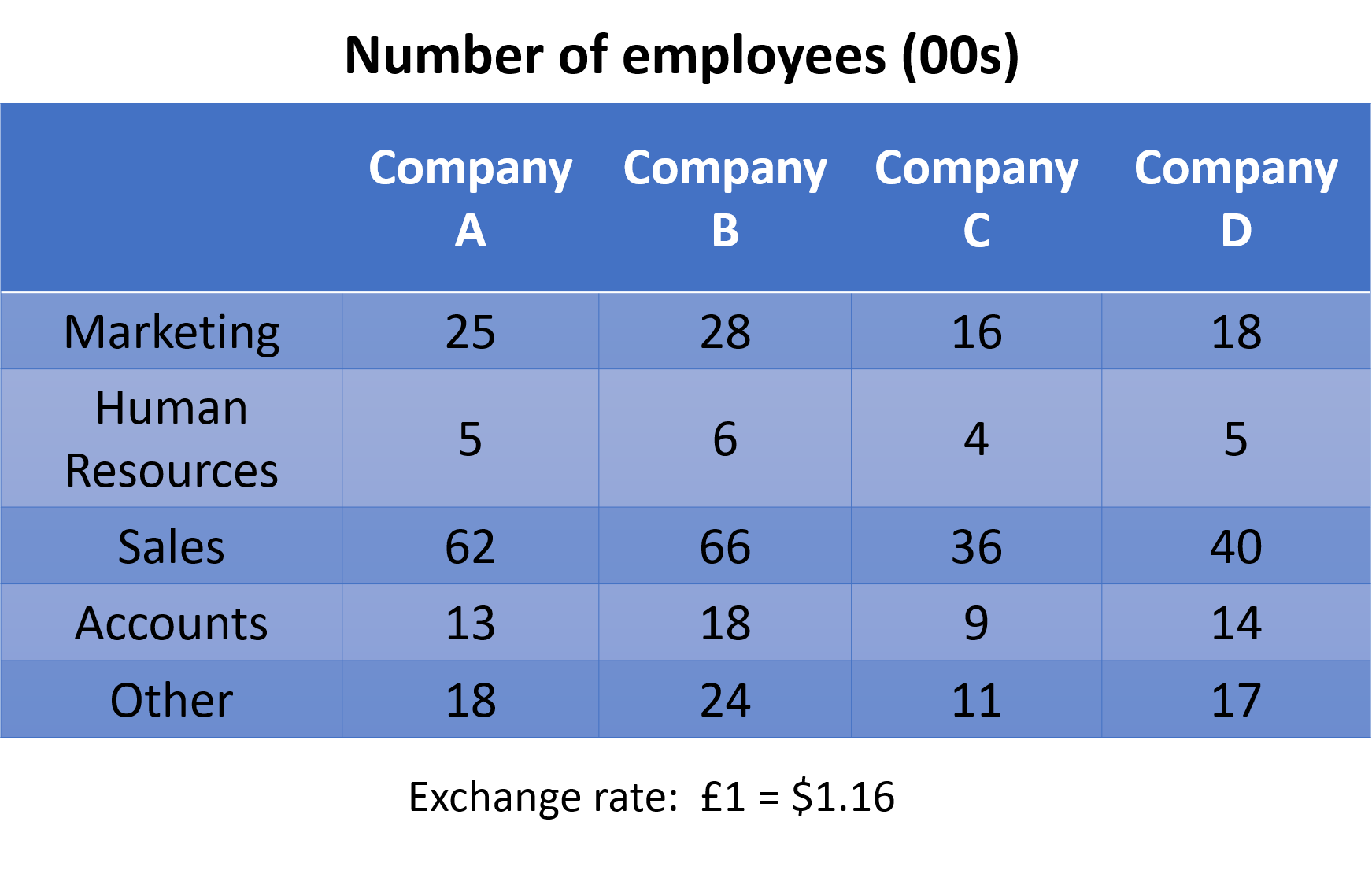
Which company had the greatest percentage of HR staff?

A: Company A

B: Company B

C: Company C

D: Company D

Written Solutions

Since this question concerns proportion and percentages, it is much more convenient to overlook the fact that the figures should be in hundreds.

In company A, there was a total of 25 + 5 + 62 + 13 + 18 = 123 employees.

Of these, 5 were HR staff.

As a percentage, this is 5 \div 123 \times 100 = 4.07\%

In company B, there was a total of 28 + 6 + 66 + 18 + 24 = 142 employees.

Of these, 6 were HR staff.

As a percentage, this is 6 \div 142 \times 100 = 4.23\%

In company C, there was a total of 16 + 4 + 36 + 9 + 11 = 76 employees.

Of these, 4 were HR staff.

As a percentage, this is 4 \div 76 \times 100 = 5.26\%

In company D, there was a total of 18 + 5 + 40 + 14 + 17 = 94 employees.

Of these, 5 were HR staff.

As a percentage, this is 5 \div 94 \times 100 = 5.32\%

Therefore, Company D had the greatest percentage of HR staff.

Question 2

What is the ratio of overall sales staff to accounts staff across all four companies?

A: 22 : 7

B: 23 : 9

C: 34 : 9

D: 36 : 7

Written Solutions

Again, since we are dealing with ratios and proportion, it is much more convenient to overlook the fact that the figures should be in hundreds.

The number of sales staff is 62 + 66 + 36 + 40 = 204

The number of accounts staff is 13 + 18 + 9 + 14 = 54

Therefore the ratio of sales staff to accounts staff is 204 : 54

This can be simplified to 34 : 9

If you type into your calculator 204 \div 54, your calculator may even display the answer \frac{34}{9}

Question 3

The percentage of directors in the marketing departments for the companies A, B, C and D was 14%, 18%, 12% and 15% respectively.  If all the directors have a combined salary of £85,540,000, how much is a director paid on average?

A: £45,000

B: £55,000

C: £65,000

D: £68,000

Written Solutions

In Company A, there are 2500 members of staff in the marketing department. If 14% are directors, then we can work out exactly how many directors this is:

2500 \times 0.14 = 350 directors

In Company B, there are 2800 members of staff in the marketing department. If 18% are directors, then we can work out exactly how many directors this is:

2800 \times 0.18 = 504 directors

In Company C, there are 1600 members of staff in the marketing department. If 12% are directors, then we can work out exactly how many directors this is:

1600 \times 0.12 = 192 directors

In Company D, there are 1800 members of staff in the marketing department. If 15% are directors, then we can work out exactly how many directors this is:

1800 \times 0.15 = 270 directors

Therefore across the 4 companies there is a total of 350 + 504 + 192 + 270 = 1316 directors.

If the combined salary of these directors is £85,540,000, then we can calculate the average salary as follows:

£85,540,000 \div 1316 = £65,000

Question 4

Company A plan to increase the number of accounts staff by 16% while Company B would like to reduce the number of accounts staff by 15%.  What will be the difference in number of accounts employees between the 2 companies if they both carry out their new staffing plans?

A: 19

B: 22

C: 26

D: 32

Written Solutions

Company A currently has 1300 accounts staff. If this is going to increase by 16%, then we can work out how many members of staff the department will have as follows:

1300 \times 1.16 = 1508

Company B currently has 1800 accounts staff. If this is going to decrease by 15%, then we can work out how many members of staff the department will have as follows:

1800 \times 0.85 = 1530

Therefore the difference in members of staff is simply 1530 - 1508 = 22

Question 5

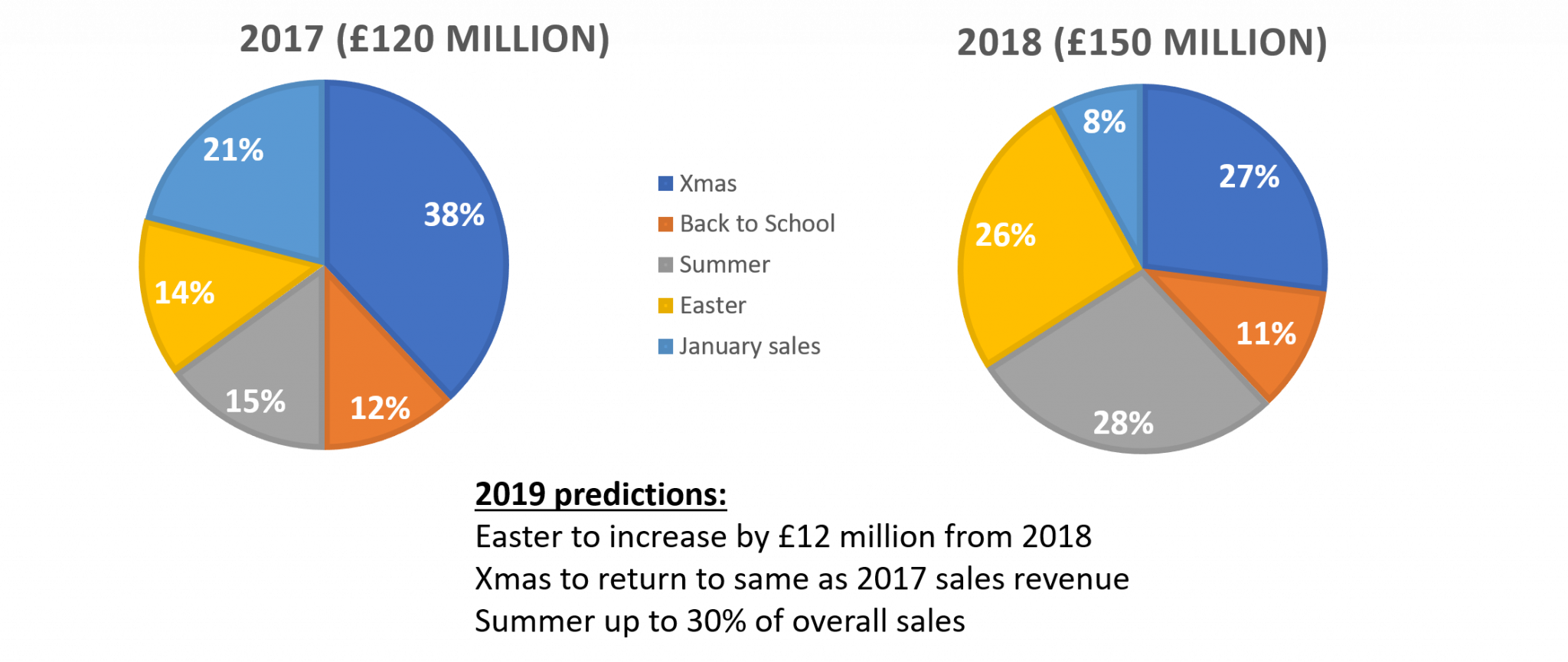
From 2017 to 2018, what was, to the nearest whole number, the percentage decrease in value of combined Xmas and January sales?

A: 24%

B: 26%

C: 28%

D: 32%

Written Solutions

In 2017, Xmas and January sales came to 59% of total sales.

The value of sales was therefore:

0.59 \times \pounds120 \text{ million} = £70.8 \text{ million}

In 2018, Xmas and January sales came to 35% of total sales.

The value of sales was therefore:

0.35 \times £150 \text{ million} = £52.5 \text{ million}

Therefore sales Xmas and January sales decreased in value from £70.8 million to £52.5 million.

As a percentage, decrease, this can be calculated as follows:

\dfrac{\pounds70.8 \text{ million}-\pounds52.5 \text{ million}}{\pounds70.8 \text{ million}} \times 100 = 25.84\% or 26\% to the nearest whole number.

Question 6

The ratio of sales overall for 2017, 2018 and 2019 is 4 : 5 : 7.  How much revenue came from back to school purchases in 2019  if it represented 9% of the total sales share?

A: £14.6 million

B: £18.9 million

C: £21.4 million

D: £22.7 million

Written Solutions

The overall sales ratio for 2017, 2018 and 2019 is 4 : 5 : 7 , which has to be a simplified version of £120 \text{ million}: £150 \text{ million} : \text{ unknown total}.

What have we done to simplify £120 (let’s forget that this is in millions) to 4? We have divided by 30. Or, looking at it form the other perspective to get from 4 to 120, you have multiplied by 30. Therefore if we multiply 7 by 30, we will work out the unknown total sales value in 2019:

30 \times 7 = \pounds210 \text{ million}

If 9% was from back to school purchases, then the exact amount can be calculated as follows:

0.09 \times \pounds210 = \pounds18.9 \text{ million}

Question 7

To the nearest whole number, what was the percentage increase between the 2017 and 2018 sales values of the category which had the smallest change in percentage share from 2017 to 2018?

A: 13%

B: 14%

C: 15%

D: 16%

Written Solutions

The category which had the biggest change in percentage share can easily be calculated as follows:

Xmas has moved from 38% to 27% which is a difference of 11 percentage points.

Back to School has moved from 12% to 11% which is a difference of 1 percentage point.

Summer has moved from 15% to 28% which is a difference of 13 percentage points.

Easter has moved from 14% to 25% which is a difference of 12 percentage points.

Xmas has moved from 21% to 8% which is a difference of 13 percentage points.

Therefore Back to School sales had the smallest change in percentage share from one year to the next.

The difference in between the sales values from one year to the next can be calculated as follows:

2017: £120 \text{ million} \times 0.12 = £14.4 \text{ million}

2018: £150 \text{ million} \times 0.11 = £16.5 \text{ million}

So the Back to School sales values went from £14.4 million to £16.5 million. As a percentage increase, this can be calculated as follows:

\dfrac{£16.5-£14.1}{£14.4} \times 100 = 14.583\% or 15\% to the nearest whole number.

Question 8

Use the prediction to calculate the 2019 value of January and back to school sales combined if overall sales increase by 22%.

A: £22.3 million

B: £25.9 million

C: £31.5 million

D: £36.8 million

Written Solutions

If overall sales increase by 22%, the total sales can be calculated as follows:

1.22 \times £150 \text{ million} = £183 \text {million}

There are no predictions for the January and back to school categories for 2019, but we do know what the prediction for the other categories are, so by deducting the three known categories from the £183 million, we can work out the combined value of January and back to school sales.

Easter increased by £12 million from 2018. In 2018, Easter sales had a value of 26%:

0.26 \times £150 = £39 \text{ million}

Therefore the Easter value was £39 \text{ million} + £12 \text{ million} = £51 \text{ million}

Xmas retuned to 2017 values which was 38% of £120 million.

0.38 \times £120 = £45.6 \text{ million}

Summer was up by 30% of overall sales. We know that the 2019 sales value was £183, so the summer sales accounted for:

£183 \text{ million} \times 0.3 = £54.9 \text{ million}

If total sales were £183 million and summer accounted foo £54.9 million, Xmas £45.6 million and Easter £39 million, then the combined January and back to school sales for 2019 can be calculated as follows:

\pounds183 - \pounds54.9 - \pounds45.6 - \pounds51 = \pounds31.5 \text{ million}

Question 9

What is the difference in value between Mr Smith’s shares in Company A and company C?

A: £16,780

B: £21,993

C: £23,360

D: £24,625

Written Solutions

Mr Smith’s Company A shares are 20% of the total which have a combined value of £320,000. Therefore, Mr Smith’s shares in Company A have a value of:

£320,000 \times 0.2 = £64,000

Mr Smith’s Company C shares are 28% of the total which have a combined value of £312,000. Therefore, Mr Smith’s shares in Company A have a value of:

£312,000 \times 0.28 = £87,360

Therefore the difference between Mr Smith’s Company A and Company C shares are:

\pounds87,360 - \pounds64,000 = \pounds23,360

Question 10

Which person has the most valuable percentage of shares for any 1 company?

A: Mr Smith

B: Mr Jones

C: Ms Williams

D: Ms Everett

Written Solutions

In order to tackle this question, we have to work out who has the greatest percentage share in each company.

In Company A, Mr Jones has the biggest percentage share, 34%. His shares are worth:

0.34 \times £320 = £108.80

In Company B, Ms Everett has the biggest percentage share, 32%. His shares are worth:

0.32 \times £186 = £59.52

(This figure probably could have been avoided altogether since this person has a smaller percentage share of a smaller overall total, so the value of the shares was logically going to be less than Mr Jones’ Company A shares.)

In Company C, Mr Smith and Ms Evertt have the biggest percentage share, 28%. These shares are worth:

0.28 \times £312 = £87.36

(This figure probably could have been avoided altogether since this person has a smaller percentage share of a smaller overall total, so the value of the shares was logically going to be less than Mr Jones’ Company A shares. It is also for two people, so can’t be the correct answer since all the answers have just the one person listed.)

In Company D, Ms Williams has the biggest percentage share, 27%. Her shares are worth:

0.27 \times £405 = £109.35

Therefore Ms Williams’ shares are the most valuable.
(Note that I didn’t worry about turning the values into thousands. By being consistent and ignoring the thousands in each calculation, I was still able to arrive at the same correct answer.)

Question 11

If Ms Everett is sold 25% of Mr Smith’s Company C shares, what will be the ratio of Ms Everett’s shares to Mr Jones’ shares in Company C?

A: 4 : 3

B: 5 : 2

C: 5 : 3

D: 7 : 5

Written Solutions

If Mr Smith has 28% of Company C shares and sells 25% of them, in other words \frac{1}{4} of them, this means that he will transfer 28 \div 4 = 7\% to Ms Everett. This means that Mr Smith now has 21% of the total shares and Ms Everett has 28 + 7 = 35\% of the overall shares.

This now means that Ms Everett and Mr Jones have shares in the ratio of 35 : 21 which can be simplified by dividing both of these numbers by 7 to 5 : 3

Question 12

If the value of Company A shares increases by 15%, and Company B’s by 18%, what is the total value of Ms Everett’s Company A and Company B shares combined to the nearest pound?

A: £103,040

B: £142,976

C: £173,274

D: £195,885

Written Solutions

The value of Company A shares is £320,000. If this increases by 15%, then the new value will be:

£320,000 \times 1.15 = £368,000

If Ms Everett’s shares are 28%, then her shares are worth:

0.28 \times £368,000 = £103,040

The value of Company B shares is £186,000. If this increases by 18%, then the new value will be:

£186,000 \times 1.18 = £219,480

If Ms Everett’s shares are worth 32%, then her shares are worth:

£219,480 \times 0.32 = £70,233.60

Therefore her shares in the two companies are worth:

£103,040 + £70,233.60 = £173,274 to the nearest pound

Question 13

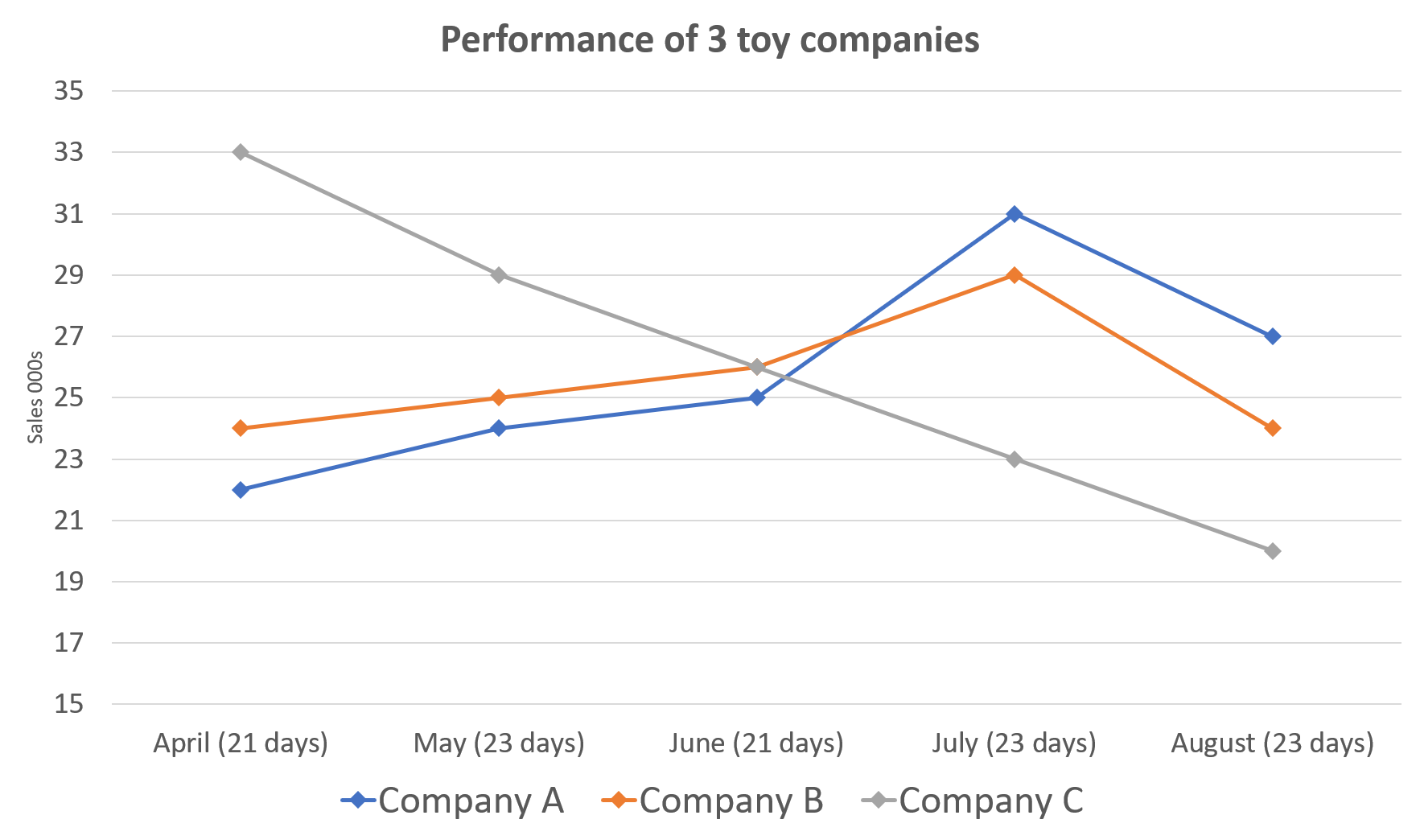
What was the approximate percentage change in sales per day of Company B from April to May?

A: 4.3% decrease

B: 4.7% increase

C: 4.9% decrease

D: 5.1% increase

Written Solutions

Note that this question is referring to sale per day whereas the chart shows the number of sales per month:

The number of sales per day in April was:

24000 \div 21 = 1142.86

The number of sales per day in May was:

25000 \div 23 = 1086.96

As a percentage decrease, this is:

\dfrac{1142.86 – 1086.96}{1142.86} \times 100 = 4.9\% \text{ decrease}

(Even if you round the figures to 1143 for April and 1087, which seems sensible, you will still arrive at an answer that is close to 4.9%.)

Question 14

If Company A sells for a £12 profit, Company B for a £10 profit and Company C generates a third of the profit of Company A per sale, what is the total profit for the 3 companies combined in June and July, assuming that 4% of the products supplied are defective and must be refunded?

A: £1,307,950

B: £1,311,245

C: £1,361,280

D: £1,363,360

Written Solutions

In June and July, Company A makes 25 + 31 = 56,000 \text{ sales}

If each sale generates £12 profit, then the total profit is 55,000 \times £12 = £672,000

If 4% of the products are defective, then this means that 96% of sales generate profit.

If 96% products generate then profit, the total profit is:

0.96 \times £672,000 = £645,120

In June and July, Company B makes 26 + 29 = 55,000 \text{ sales}

If each sale generates £10 profit, then the total profit is 55,000 \times £10 = £550,000

If 4% of the products are defective, then this means that 96% of sales generate profit.

If 96% products generate then profit, the total profit is:

0.96 \times £550,000 = £528,000

In June and July, Company C makes 26 + 23 = 49,000 \text{ sales}

If each sale generates a third of company Am the each sale generates £4 profit, so the total profit is 49,000 \times £4 = £196,000

If 4% of the products are defective, then this means that 96% of sales generate profit.

If 96% products generate then profit, the total profit is:

0.96 \times £550,000 = £188,160

Therefore the total generated by all three companies is:

£645,120 + £528,000 + £188,160 = £1,361,280

Question 15

Company A sells at £600 per batch of 50.  If the batch size increases by 22% in May and the selling price remains the same, what is the approximate difference in revenue generated by Company A between April and May?

A: £19,000

B: £21,000

C: £26,000

D: £28,000

Written Solutions

In April, Company A sells 22,000 toys. If they are sold in batches of 50, then they will have 22,000 \div 50 = 440 batches. If each batch sells for £600, then they will make 440 \times £600 = £264,000

If the batch size increase by 22%, then the new batch size will be:

50 \times 0.22 = 61

In May, there are 24,000 toys sold. If they are sold in batches of 61, then they will have 24,000 \div 61 = 393 batches. If each batch sells for £600, then they will make 393 \times £600 = £235,800£264,000 - £235,800 = £28,200 or £28,000 to the given approximation.

Question 16

What was Company A’s percentage of overall sales from April to August to the nearest whole number?

A: 26%

B: 29%

C: 33%

D: 35%

Written Solutions

Since this is a percentage question, it is worth overlooking the fact that the graph shows thousands of sales.

Between April and August, Company A made 22 + 24 + 25 + 31 + 27 = 129 \text{ sales}.

Between April and August, Company B made 24 + 25 + 26 + 29 + 24 = 128 \text{ sales}.

Between April and August, Company C made 33 + 29 + 26 + 23 + 20 = 131 \text{ sales}.

The total sales were 129 + 128 + 131 = 388

Therefore Company A’s percentage of overall saes was:

129 \div 388 \times 100 = 33.24\% or 33\% to the nearest whole number.

Question 17

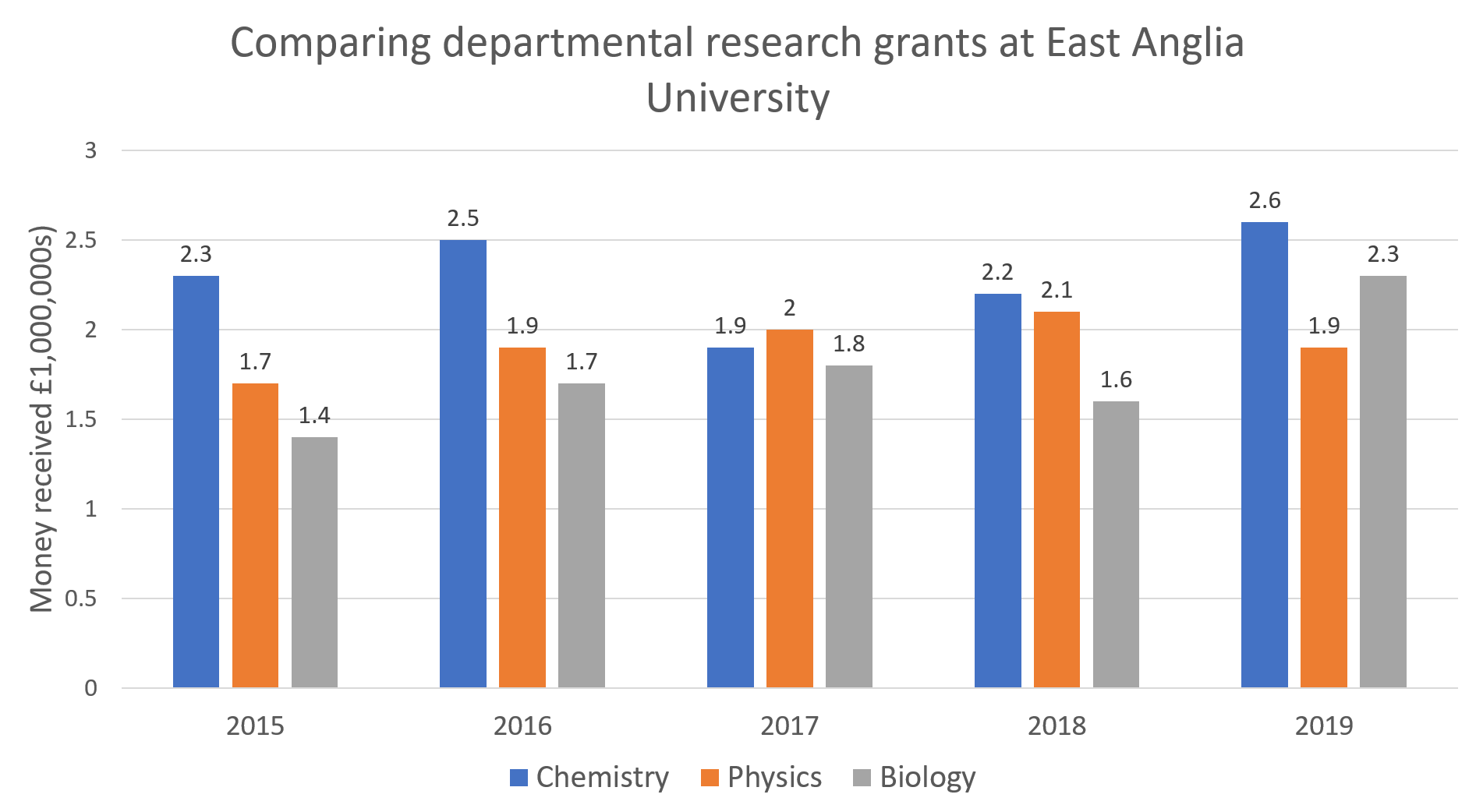
As a percentage decrease to one decimal place, how much did the university save in research grants between 2016 and 2017?

A: 4.9%

B: 6.6%

C: 8.2%

D: 11.6%

Written Solutions

In 2016, the university spent 2.5 + 1.9 + 1.7 = £6.1 \text{ million}

In 2017, the university spent 1.9 + 2 + 1.8 = £5.7 \text{ million}

Therefore the university saved £6.1 \text{ million} - £5.7 \text{ million} = £0.4 \text{ million}

As a percentage decrease, this can be calculated as follows:

\dfrac{\pounds0.4}{\pounds6.1} \times 100 = 6.6\% \text{ to one decimal place}

Question 18

In 2015, physics grants were split between postgraduate and postdoctorate research in the ratio of 5 : 11. If there were 18 postgraduate students in total, how much, to the nearest hundred pounds, was their grant per year if the postgraduate grant was spread over a three year period?

A: £9,800

B: £11,400

C: £13,900

D: £16,600

Written Solutions

In 2015, physics grants came to a total of £1.7 million. If the ratio between postgraduate and postdoctorate grants was split in the ratio of 5 : 11 , then this means that \frac{5}{16} were postgraduate grants. (We are dealing with sixteenths here because 5 + 11 = 16 . Now, that we can know what fraction of the total comprised postgraduate grants, we can work out how much the postgraduate grants came to:

£1.7 \text{ million} \times \frac{5}{16} = £0.53125 \text{ million}

If this amount was shared between 18 students, then each person would receive:

£0.53125 \times 1,000,000 \div 18 = £29,513.88

If this is how much they receive over a three-year period, then we can easily calculate how much they receive per year:

£29513.88 \div 3 = £9837.96 or £9,800 to the nearest given approximation.

Question 19

All 50 biology researchers must perform some teaching duties. If three quarters of all biology grant money in 2019 was used to pay them for their research, and they earned £23 per hour of research, how many hours of research does each researcher undertake?

A: 1080 hours

B: 1365 hours

C: 1500 hours

D: 1620 hours

Written Solutions

In 2019, the biology grants came to a total of £2.3 million. \frac{3}{4}[\latex] of this money was used to pay for research, so the cost of this research was:</p> <p>[latex]£2.3 \text{ million} \times \frac{3}{4} =£1.725 million

If the researchers are paid £23 per hour, then we can work out how many hours of teaching in total are undertaken:

£1.725 \times 1,000,000 \div £23 = 75,000 hours

If there are 50 biology researchers in total, then each researcher must have done the following number of hours:

75,000 \div 50 = 1500 hours

Question 20

In 2017, the maths department received 5% less money in grants than the physics department, but their total then increased by 8% each subsequent year. What is the percentage growth in the total value of grants given to all 4 departments (physics, chemistry, biology, maths) from 2017 to 2019 to one decimal place?

A: 18.6%

B: 19.4%

C: 20.2%

D: 21.0%

Written Solutions

In 2017, the physics department received £2 million. If the maths department received 5% less, then the amount that the maths department received can be calculated as follows:

£2 \text{ million} \div 0.95 = £1.9 \text{ million}

Therefore, if the maths department received 8% extra in 2018, the maths department would have received:

£1.9 \text{ million} \times 1.08 = £2.052 \text{ million}

In 2019, the maths would have received even more grant money than the year previous as the 8% increase came into effect again:

£2.052 \text{ million} \times 1.08 = £2.21616 \text{ million}

In 2017, the total of all grants was:

£1.9 \text{ million (physics)} + £2 \text{ million (chemistry)} + £1.8 \text{ million (biology)} + £1.9 \text{ million (maths)} = £7.6 \text{ million}

In 2019, the total of all grants was £2.6 \text{ million (physics)} + £1.9 \text{ million (chemistry)} + £2.3 \text{ million (biology)} + £2.21616 \text{ million (maths)} = £9.01616 \text{ million}

If the grants increased from £7.6 million to £9.01616, then as a percentage increase, this can be calculated as follows:

\dfrac{\pounds9.01616 \text{ million} - \pounds7.6 \text{ million}}{\pounds7.6 \text{ million}} \times 100 = 18.63\% or 18.6\% to the nearest given approximation.