Question 1

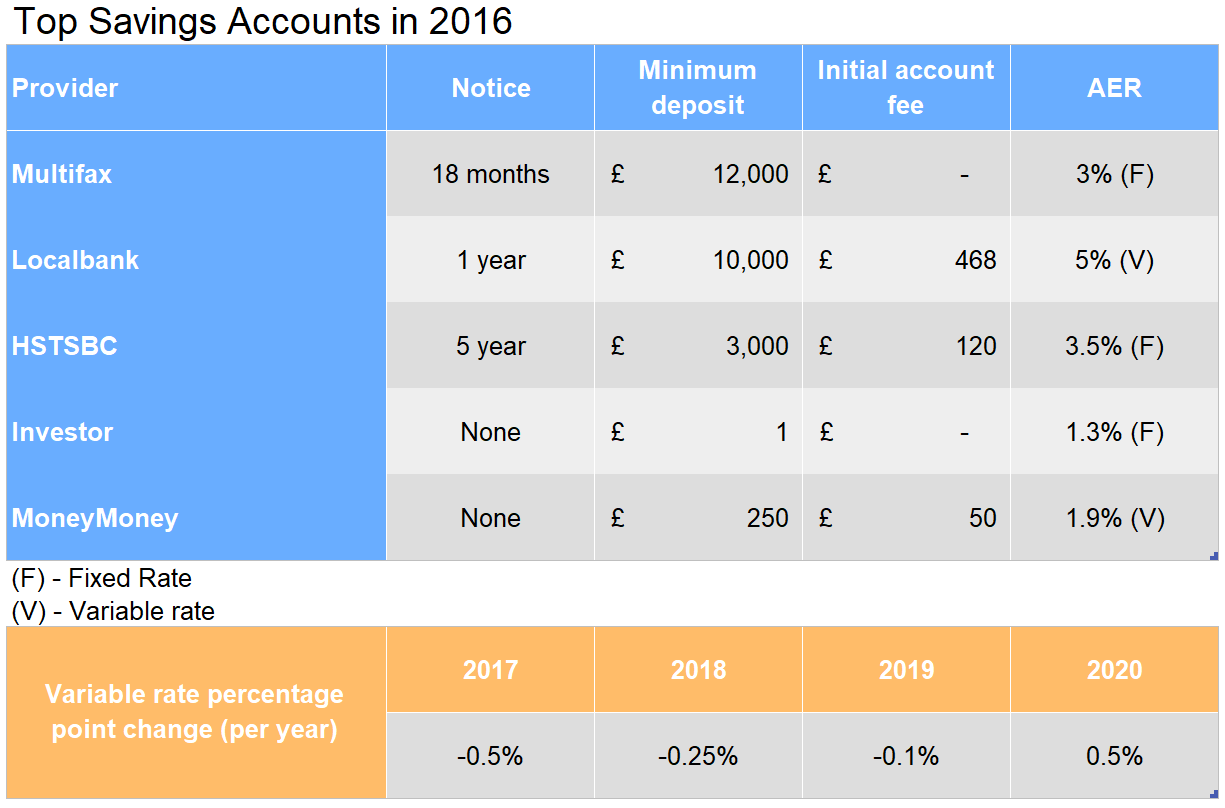
What is the percentage change in value over 3 years in a deposit of £12,000 at Localbank?

                A: 10.5% increase

                B: 9.9% increase

                C: 9.0% increase

                D: 9.4% increase

Written Solutions

Step 1: First subtract the initial account fee. \pounds12,000 - \pounds468 = \pounds11,532

Step 2: Next we need to use the starting AER and adjust it each year by the percentage point change for 2017 and 2018. For example, in 2017 the new AER is 5\% - 0.5\% = 4.5\%. Now use the multiplier to adjust the value of the deposit each year. E.g. in 2016 the multiplier is 1.05 for a 5% increase.

\begin{aligned}\text{2016: }& \pounds11,532 \times 1.05 = \pounds12,108.60 \\ \text{2017: }& \pounds12,108.60 \times 1.045 = \pounds12,653.49 \\ \text{2018: }& \pounds12,653.49 \times 1.0425 = \pounds13,191.26 \end{aligned}

Step 3: Calculate the percentage change as below.

\dfrac{\text{New} - \text{Old}}{\text{Old}} \times 100 \equiv \dfrac{\pounds13,191.26 - \pounds12,000}{\pounds12,000} \times 100 = \bold{9.9\%\text{ increase}}

Question 2

£8,000 is deposited into HSTSBC and Investor in the ratio 2:3. After two years what is the ratio of savings in each account?

                A: 1: 1.49

                B: 1: 1.53

                C: 1: 1.57

                D: 1: 1.45

Written Solutions

Step 1:  First we need to find out the initial split of money. The ratio 2: 3 has 5 parts.

\pounds8,000 \div 5 = \pounds1,600

\begin{aligned}\text{HSTSBC} &: \text{Investor} \\ 2 &: 3 \\ 2 \times \pounds1,600 &: 3 \times \pounds1,600 \\ \pounds3,200 &: \pounds4,800 \end{aligned}

Step 2: We need to calculate two years of savings increases for the two banks. But first reduce the savings in HSTSBC by £120 for the initial account fee.

\pounds3,200 - \pounds120 = \pounds3,080

We need to apply the AER, these are 3.5% and 1.3% which correspond to multipliers of 1.035 and 1.013 respectively. Since the interest is accrued over two years we need to apply the multiplier twice – \times1.035 \times 1.035 \equiv \times1.035^2

\begin{aligned}\text{HSTSBC} &: \text{Investor} \\ \pounds3,080 &: \pounds4,800 \\ \pounds3,080 \times 1.035^2 &: \pounds4,800 \times 1.013^2 \\ \pounds3,299.37 &: \pounds4,925.61\end{aligned}

Step 3: Finally, simplify the ratio by dividing through by the smallest portion.

\begin{aligned}\text{HSTSBC} &: \text{Investor} \\ \pounds3,299.37 &: \pounds4,925.61 \\ \dfrac{3299.37}{3299.37} &: \dfrac{4925.61}{3299.37} \\ 1 &: 1.49\end{aligned}

Question 3

£500 is deposited into MoneyMoney. After 5 years, what proportion of the money in the account was accrued due to interest?

                A: 9.0%

                B: 2.9%

                C: 5.7%

                D: 6.8%

Written Solutions

Step 1: Subtract the initial account fee from the deposit \pounds500 - \pounds50 =\pounds450

Step 2: Adjust this value by the multiplier for each of the 5 years. The AER for each year are: 1.9%, 1.4%, 1.15%, 1.05% and 1.55%. These correspond to multipliers of 1.019, 1.014, 1.0115, 1.0105 and 1.0155 respectively.

\pounds450 \times 1.019 \times 1.014 \times 1.0115 \times 1.0105 \times 1.0155 = \pounds482.62

So, this means \pounds482.62 - \pounds450 = \pounds32.62 was accrued from interest.

Step 3: Now calculate the proportion by dividing the interest by the total, then multiplying by 100 to express it as a percentage.

\dfrac{\pounds32.62}{\pounds482.62} \times 100 = \bold{6.8\%}

Question 4

£12,000 is saved in both Multifax and HSTSBC. What is the difference in value of these two deposits after 4 years?

                A: £264.17

                B: £126.46

                C: £98.70

                D: £185.43

Written Solutions

Step 1: The value of the deposit in Multifax is increased by a fixed AER of 3% each year. This is a multiplier of 1.03 over four years.

\pounds12,000 \times 1.03^4 = \pounds13,506.11

Step 2: We first need to reduce the value of the deposit in HSTSBC by £120 for the initial account fee, leaving £11,880. Then there is a fixed AER of 3.5%, or a multiplier of 1.035 over four years.

\pounds11,880 \times 1.035^4 = \pounds13,632.57

Step 3: Find the difference between the two deposits.

\pounds13,632.57 - \pounds13,506.11 \approx \bold{\pounds126.46}

Question 5

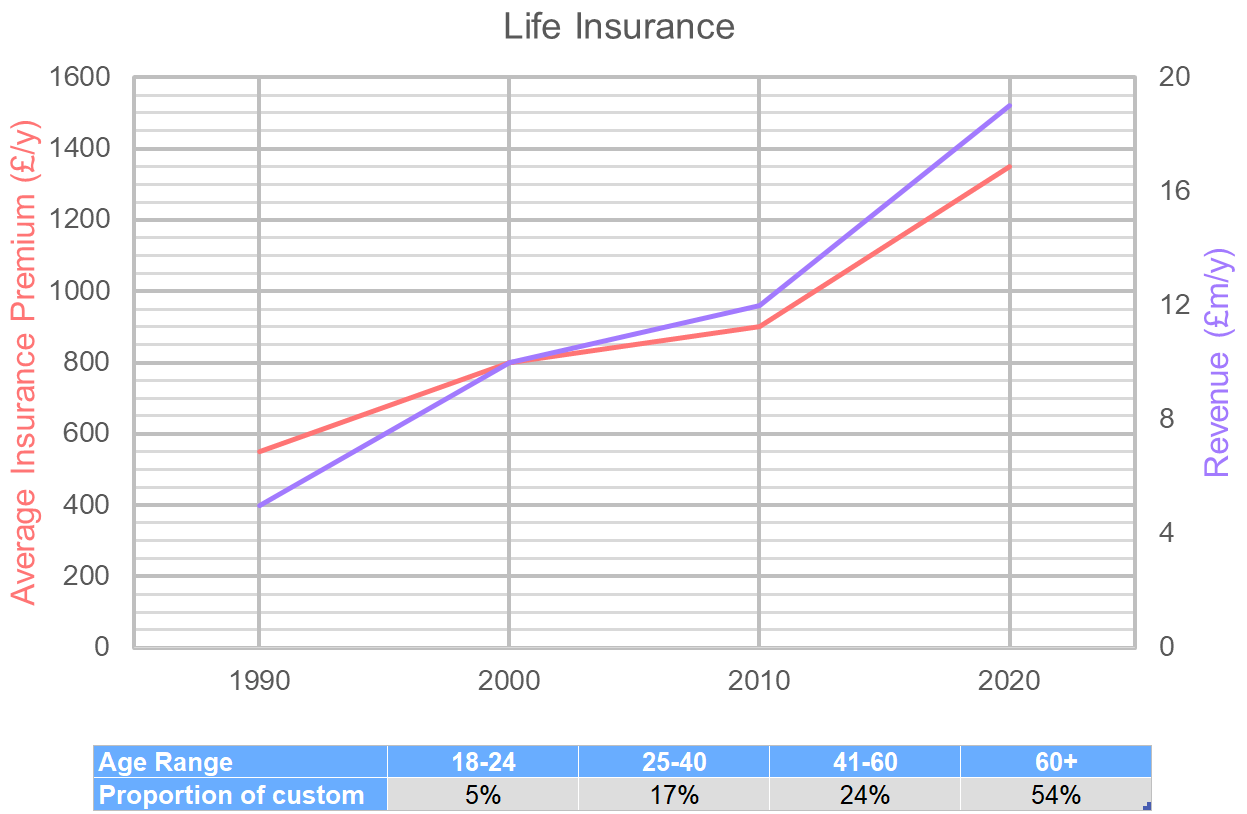
What is the ratio of the number of customers in 2000, 2010 and 2020?

                A: 1: 1.09: 1.10

                B: 1: 1.06: 1.24

                C: 1: 1.04: 1.30

                D: 1: 1.07: 1.13

Written Solutions

Step 1: Divide revenue by the average insurance premium in each decade to get the number of customers for that period.

\begin{aligned}\dfrac{\pounds10\text{m}}{\pounds800} &= 12,500 \\ \dfrac{\pounds12\text{M}}{\pounds900} &= 13,333 \\ \dfrac{\pounds19\text{m}}{\pounds1,350} &= 14,074 \end{aligned}

Step 2: Form the ratio and simplify.

\begin{gathered}2000 : 2010 : 2020 \\ 12,500: 13,333: 14,074 \\ \dfrac{12,500}{12,500}: \dfrac{13,333}{12,500}: \dfrac{14,074}{12,500} \\ 1: 1.07: 1.13\end{gathered}

Question 6

Costs start at 13% of revenue in 1990, rising by 5 percentage points per decade, with an additional 20 percentage points increase in 2020. In which year were profits highest?

                A: 1990

                B: 2000

                C: 2010

                D: 2020

Written Solutions

Step 1: Work out the percentage decrease due to costs in each decade. For example, there is a 13% decrease in revenue in 1990, leaving us with 87% of revenue as profit.

\begin{aligned}\text{1990: }&13\%\text{ decrease or a multiplier of }0.87 \\ \text{2000: }&13\% + 5\% = 18\%\text{ decrease or a multiplier of }0.82 \\ \text{2010: }&13\%+10\%=23\%\text{ decrease or a multiplier of }0.77 \\ \text{2020: }&13\%+35\% =48\%\text{ decrease or a multiplier of }0.52\end{aligned}

Step 2: Apply the multiplier to the revenue for each decade to calculate total profit and select our answer.

\begin{aligned}\text{1990: }&0.87 \times \pounds5\text{m} = \pounds4.35\text{m} \\ \text{2000: }&0.82 \times \pounds10\text{m} = \pounds8.20\text{m} \\ \text{2010: }&0.77 \times \pounds12\text{m} = \pounds9.24\text{m} \\ \text{2020: }&0.52 \times \pounds19\text{m} = \bold{\pounds9.88\text{m}}\end{aligned}

Question 7

If the percentage increase in revenue from 2010 to 2020 continues, what will the revenue in 2030 be as a proportion of the total revenue from 1990 to 2030?

                A: 37.4%

                B: 36.1%

                C: 39.6%

                D: 38.2%

Written Solutions

Step 1: Calculate the percentage increase in revenue from 2010 to 2020.

\dfrac{\pounds19\text{m} - \pounds12\text{m}}{\pounds12\text{m}} \times 100 \approx 58.3\%

Step 2: This corresponds to a multiplier of 1.583, apply this to the revenue in 2020 to get an estimate of the revenue in 2030.

\pounds19\text{m} \times 1.583 \approx \pounds30.1\text{m}

Step 3: Find the sum of all revenue from 1990 to 2030 and find the 2030 revenue as a proportion of the total.

\dfrac{\text{2030 Revenue}}{\text{Total Revenue from 1990 to 2030}} \times 100 \equiv \dfrac{\pounds30.1\text{m}}{\pounds76.1\text{m}} \times 100 \approx \bold{39.6\%}

Question 8

In 2000 the average insurance premium for those age 41+ was £920. What was the average insurance premium for those younger than 41?

                A: £374.55

                B: £365.07

                C: £395.95

                D: £382.90

Written Solutions

Step 1: First we need to calculate the number of customers – we can do this by dividing the revenue by the overall average price of an insurance premium, £800.

\text{Number of customers} = \pounds10\text{m} \div \pounds800 = 12,500\text{ customers}

From the table, we know that 78% of these customers were aged 41+, so we can calculate the number of customers age 41+ by using the multiplier 0.78.

12,500 \times 0.78 = 9,750

Step 2: Now that we know the number of customers aged 41+ (and conversely the number younger than 41 – 2,750) we can multiply this by the average premium for the age bracket, £920, to calculate the revenue from customers over the age of 41.

9,750 \times \pounds920 = \pounds8.97\text{m}

The remainder of the revenue, \pounds10\text{m} - \pounds8.97\text{m} = \pounds1.03\text{m} must be generated by those under the age of 41. We just need to divide the revenue by the number of people to calculate the average.

\dfrac{\text{Revenue from customers under 41}}{\text{Number of customers under 41}} = \dfrac{\pounds1.03\text{m}}{2,750} \approx \bold{\pounds374.55}

Question 9

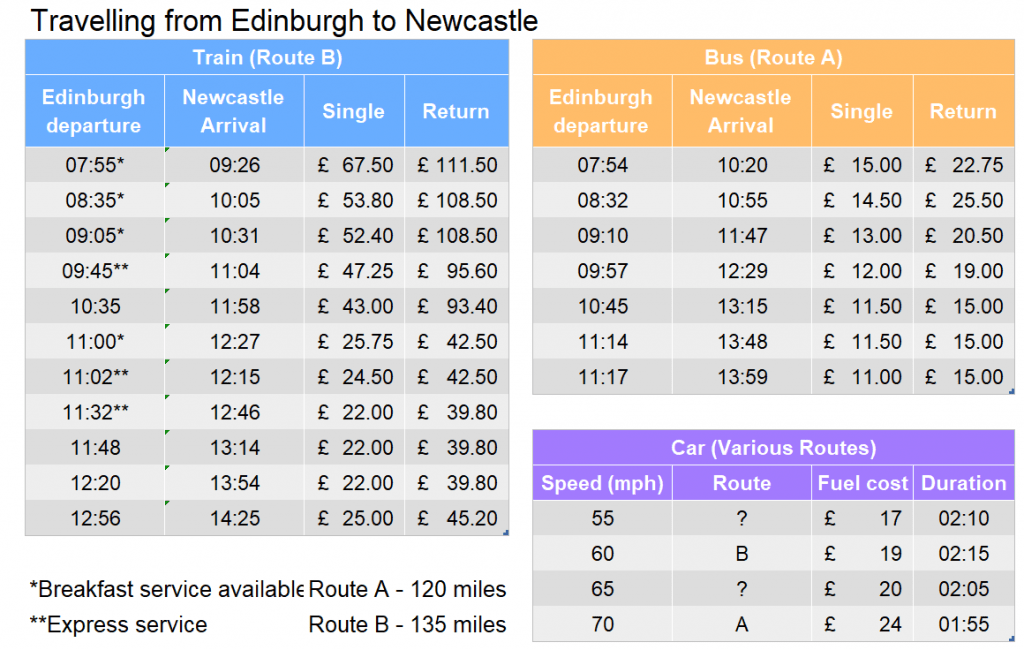
A group of four plan to travel on the cheapest bus from Edinburgh to Newcastle. Instead they must take the cheapest car journey along the same route. What is the percentage change in the price per person?

                A: 72% decrease

                B: 61% decrease

                C: 55% decrease

                D: 45% decrease

Written Solutions

Step 1: The price per person on the cheapest bus is £11.00 for a single, read from the table.

Step 2: We need to check whether the 55mph and 65mph cars take route A. To do this we calculate the distance, using the formula below. We write the time as a fraction of the time in minutes divided by the number of minutes in an hour. This means that it multiplies the speed by the fraction of hours, in the first case around 2.17 rather than the 24 hour time 02:10.

\text{Distance} = \text{Speed} \times \text{Time}

\begin{aligned}\text{55mph: }& \text{Distance} = 55 \times \left(\dfrac{130\text{ minutes}}{60\text{ minutes}}\right) \approx 119\text{ miles (Route A) }\checkmark \\ \text{65mph: }& \text{Distance} = 65 \times \left(\dfrac{125\text{ minutes}}{60\text{ minutes}}\right) \approx 135\text{ miles} \text{ (Route B)} \end{aligned}

So, the 55mph and 70mph cars task route A, with the cheapest of the two being £17. This is split over the group of four, so comes to \pounds17 \div 4 = \pounds4.25 each.

Step 3: Now we just need to calculate the percentage change from the original cost of £11 per person to £4.25 per person.

\dfrac{\pounds4.25 - \pounds11}{\pounds11} \times 100 = \bold{61\%\text{ decrease}}

Question 10

What is the combined cost of a single ticket on the fastest train with breakfast, and the fastest bus, that both arrive before 12:30. There is a discount of 24% to be deducted from the combined cost of travel.

                A: £50.84

                B: £30.59

                C: £62.70

                D: £45.87

Written Solutions

Step 1: By inspection the fastest train that arrives before 12:30 and serves breakfast is the 09:05 at 01:26 in duration. This costs £52.40.

Step 2: By inspection the fastest bus route that arrives before 12:30 is the 08:32 at 02:23 in duration. This costs £14.50.

Step 3: Now we need to reduce the total by 24%, this is a multiplier of 0.76.

\pounds52.40 + \pounds14.50 = \pounds66.90

\pounds66.90 \times 0.76 = \bold{\pounds50.84}

Question 11

What is the difference in price between a return on the fastest express train, and the fastest journey that leaves by Bus after 9:30 and returns by the fastest route B car?

                A: £11

                B: £12

                C: £13

                D: £14

Written Solutions

Step 1: By inspection the fastest express service train is the 11:02 for £42.50.

Step 2: By inspection the fastest Bus after 9:30 is the 10:45 for £11.50.

Step 3: For this step we need to check which cars take route B. We use the formula:

\text{Distance} = \text{Speed} \times \text{Time}

We must convert the 24-hour time into a fraction of hours. To do this we divide the time in minutes by 60 minutes in an hour.

\begin{aligned}\text{55mph: }& \text{Distance} = 55 \times \left(\dfrac{130\text{ minutes}}{60\text{ minutes}}\right) \approx 119\text{ miles (Route A)} \\ \text{65mph: }& \text{Distance} = 65 \times \left(\dfrac{125\text{ minutes}}{60\text{ minutes}}\right) \approx 135\text{ miles} \text{ (Route B) }\checkmark \end{aligned}

The fastest route B car journey is at 65mph for £20.

Step 4: Find the difference between the price of the train journey and the combined price of the bus and car journeys.

\pounds42.50 - (\pounds11.50 + \pounds20) = \bold{\pounds11.00}

Question 12

What is the ratio of speeds of the following: The last breakfast train, the most expensive bus, and the usual slowest route B car subject to delays that reduce the average speed by 8%.

                A: 1.84: 1: 1.17

                B: 1.79: 1: 1.08

                C: 1.82: 1: 1.19

                D: 1.89: 1: 1.12

Written Solutions

Step 1: The last breakfast train is the 11:00 that takes 01:27 to reach Newcastle. The speed of this train is therefore:

135\text{ miles} \div (87 \div 60) = 93.1\text{ mph} (We convert 24 hour time into a fraction of hours)

Step 2: The most expensive bus is the 07:54 that lasts for 02:26. The speed of the bus is:

120\text{ miles} \div (\dfrac{146}{60}) = 49.3\text{ mph}

Step 3: The slowest route B car is the 60mph car, regardless of whether 55mph and 65 mph follow route B since it is the slowest overall route. We must reduce this speed by 8%, which is a multiplier of 0.92.

60\text{ mph} \times0.92 = 55.2\text{ mph}

Step 4: Finally, form the ratio and simplify.

\begin{gathered}\text{Train}:\text{Bus}:\text{Car} \\ 93.1: 49.3: 55.2 \\ \dfrac{93.1}{49.3}:\dfrac{49.3}{49.3}:\dfrac{55.2}{49.3} \\ 1.89: 1: 1.12 \end{gathered}

Question 13

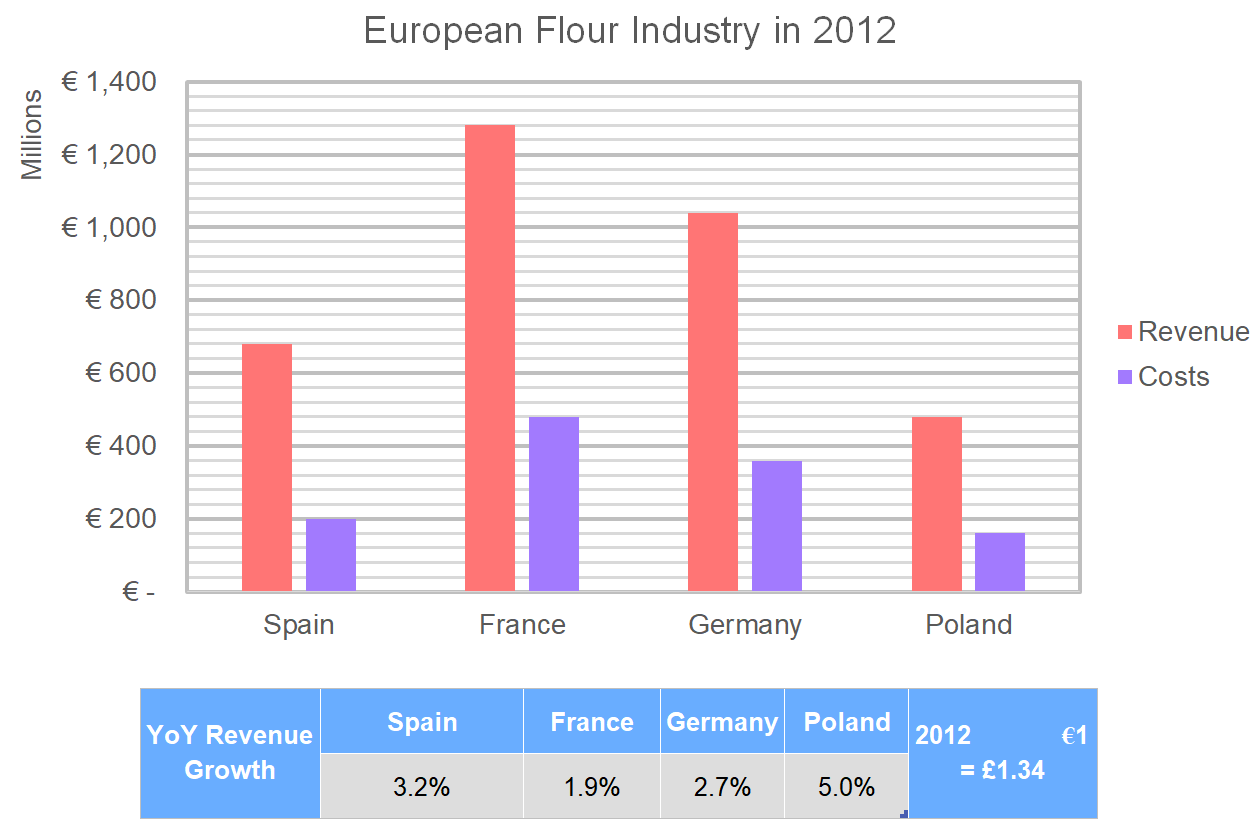
What was the percentage decrease in profits for Spain from 2012 to 2013 if costs also increased by 15%?

                A: 1.51%

                B: 1.63%

                C: 1.72%

                D: 1.84%

Written Solutions

Step 1: Calculate the costs in 2013. We increase the 2012 figures by 15%, or a multiplier of 1.15.

200\text{m euros} \times 1.15 = 230\text{m euros}

Step 2: Calculate revenue in 2013 by using the multiplier 1.032, which corresponds to an increase of 3.2%.

680\text{m euros} \times 1.032 = 701.76\text{m euros}

Step 3: Work out profit for both 2012 and 2013 by taking costs away from revenue, then calculate the percentage decrease.

\begin{aligned}\text{2012: }&\text{Profit} = 680 - 200 = 480\text{m euros} \\ \text{2013: }&\text{Profit} = 701.76 - 230 = 471.76\text{m euros} \end{aligned}

\dfrac{471.76 - 480}{480} \times 100 = \bold{1.72\%\text{ decrease}}

Question 14

Which countries profit is highest as a proportion of revenue in 2012?

                A: Spain

                B: France

                C: Germany

                D: Poland

Written Solutions

Step 1: Calculate profit for all four countries.

\begin{aligned}\text{Spain: }&680 - 200 = 480\text{m euros} \\ \text{France: }&1280 - 480 = 800\text{m euros} \\ \text{Germany: }&1040 - 360 = 680\text{m euros} \\ \text{Poland: }&480 - 160 = 320\text{m euros} \end{aligned}

Step 2: Work out the profit as a proportion of revenue by dividing profit by revenue for each country and multiplying by 100 to express it as a percentage.

\begin{aligned}\text{Spain: }&\dfrac{480}{680} \times 100 \approx \bold{70.6\%} \checkmark \\ \text{France: }&\dfrac{800}{1280} \times 100 = 62.5\% \\ \text{Germany: }&\dfrac{680}{1040} \times 100 \approx 65.4\% \\ \text{Poland: }&\dfrac{320}{480} \times 100 \approx 66.7\% \end{aligned}

Question 15

The UK has revenue of £687m in 2012 and costs of €65 for every £1000 of revenue. What is the overall profit for the UK in euros to the nearest million?

                A: €479m

                B: €468m

                C: €452m

                D: €486m

Written Solutions

Step 1: Convert the €65 into pounds so we can work out the total costs.

65 \times 1.34 = \pounds87.10

Next, divide the £687m by 1000 to figure out how many times the £87.10 needs to be paid, then multiply to calculate the total costs.

\pounds687\text{m} \div \pounds1000 = 687,000

687,000 \times \pounds87.10 \approx \pounds59.84\text{m}

Step 2: Subtract costs from revenue to calculate profit, then convert back into euros by dividing by 1.34.

\pounds687\text{m} - \pounds59.84\text{m} = \pounds627.16\text{m}

\pounds627.16\text{m} \div 1.34 \approx \bold{468\text{m euros}}

Question 16

What is the difference in profit of Spain and France after 2 years of growth, to the nearest million? Costs also grow by 12% over the period.

                A: €287m

                B: €291m

                C: €289m

                D: €293m

Written Solutions

Step 1: The revenue increases twice over two years, so we use the corresponding multiplier twice. In the case of Spain it is a 3.2% increase, so a multiplier of 1.032. Over two years this is a multiplier of \times1.032^2 = \times1.032\times1.032.

\begin{aligned}\text{Spain: }&680\text{m} \times 1.032^2 \approx 724.22\text{m} \\ \text{France: }&1,280\text{m} \times 1.019^2 \approx 1,329.10\text{m} \end{aligned}

Step 2: Calculate the new costs for each country. Costs increase by a flat 12%, which is a multiplier of 1.12.

\begin{aligned}\text{Spain: }&200\text{m} \times 1.12 = 224\text{m} \\ \text{France: }&480 \times 1.12 = 537.6\text{m} \end{aligned}

Step 3: Calculate the profit for both countries, then find the difference.

\begin{aligned}\text{Spain: }&724.22\text{m} - 224\text{m} = 500.22\text{m} \\ \text{France: }&1,329.10\text{m} - 537.6\text{m} = 791.5\text{m}\end{aligned}

791.5\text{m} - 500.22\text{m} \approx \bold{291\text{m euros}}

Question 17

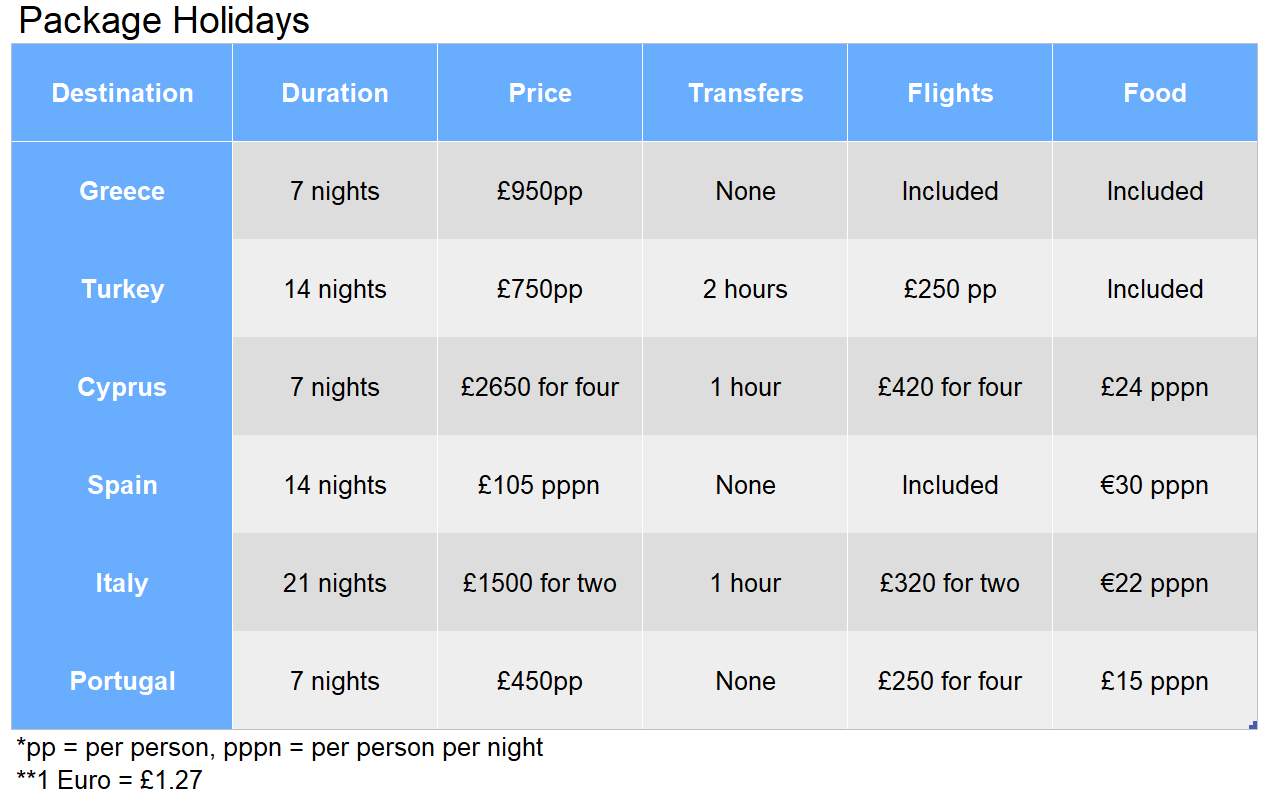
The stated price of a holiday to Cyprus increases by 27%. What is the overall percentage increase in the price per person per night with flights and food included?

                A: 17.5%

                B: 18.1%

                C: 18.7%

                D: 19.1%

Written Solutions

Step 1: First calculate the overall price per person per night. Each cost that is not already as pppn must be divided by 4 (per person) and 7 (per night).

\dfrac{\pounds2,650}{7\times4}+\dfrac{\pounds420}{7\times4} + \pounds24 = \pounds133.64

Step 2: Now do the same, but first increase the initial price for four by 27%, or a multiplier of 1.27.

\pounds2,650 \times 1.27 = \pounds3,365.50

\dfrac{\pounds3,365.50}{7\times4}+\dfrac{\pounds420}{7\times4} + \pounds24 = \pounds159.20

Step 3: Find the percentage increase.

\dfrac{\pounds159.20-\pounds133.64}{\pounds133.64} \times 100 \approx \bold{19.1\%}

Question 18

Two couples split the initial cost of a trip to Portugal in the ratio 2:3. All other costs are shared evenly. What is the overall ratio of cost between the two couples?

                A: 1: 1.42

                B: 1: 1.50

                C: 1: 1.34

                D: 1: 1.44

Written Solutions

Step 1: Share the initial cost of £450pp, or £1,800 total between the couples in the ratio 2: 3. The ratio has 5 parts, so if we split £1,800 into 5 we can then assign two shares to couple A, and three shares to couple B.

\pounds1,800 \div 5 = \pounds360

\begin{aligned}\text{Couple A}&:\text{Couple B} \\ 2&:3 \\ 2 \times \pounds360 &: 3 \times \pounds360 \\ \pounds720 &: \pounds1,080 \end{aligned}

Step 2: Next we need to add on the other costs, Flights are \pounds250 \div 2 = \pounds125 per couple and food costs \pounds15 \times 7 \times 2 = \pounds210 per couple. This is a total of \pounds335 to add to each couples total.

\begin{aligned}\text{Couple A}&:\text{Couple B} \\ \pounds720 &: \pounds1,080 \\ \pounds720 + \pounds335 &: \pounds1,080 + \pounds335 \\ \pounds1,055 &: \pounds1,415 \end{aligned}

Step 3: Finally, divide through by the lower of the two values to simplify the ratio and obtain our answer.

\begin{aligned}\text{Couple A}&:\text{Couple B} \\ \pounds1,055 &: \pounds1,415 \\ \dfrac{\pounds1,055}{\pounds1,055} &: \dfrac{\pounds1,415}{\pounds1,055} \\ 1 &: 1.34 \end{aligned}

Question 19

What is the difference between the overall price per night per person in euros for holidays to Spain or Italy?

                A: €59.32

                B: €53.80

                C: €52.47

                D: €56.56

Written Solutions

Step 1: The overall cost of a holiday to Spain pppn requires us to first convert the basic cost of £105 into euros. We must divide by the exchange rate of 1.27.

\pounds105 \div 1.27 \approx 82.68\text{ euros}

The total price pppn is therefore

82.68 + 30 = 112.68\text{ euros}

Step 2: Now calculate the same for Italy. In this case we must divide the prices by two to get the price for a single person, and then by 21 to get the price per night. Finally, we need to convert to euros by dividing by 1.27. We can write this all as a single fraction, as below.

\dfrac{\pounds1,500}{21 \times 2 \times 1.27} \approx 28.12\text{ euros pppn}

Do the same for the cost of flights, then add up all three prices pppn.

\dfrac{\pounds320}{21 \times 2 \times 1.27} \approx 6.00\text{ euros pppn}

28.12 + 6 + 22 = 56.12\text{ euros pppn}

Step 3: Now calculate the difference between the two costs pppn.

112.68 - 56.12 = \bold{56.56\text{ euros pppn}}

Question 20

What is the lowest price per person per night in GBP for a group of 8 people, with no transfers, up to 14 nights stay, with flights and food either included or paid for?

                A: £92.45

                B: £88.21

                C: £135.71

                D: £104.56

Written Solutions

Step 1: Identify which holidays fit the description. Turkey, Cyprus and Italy are out since they all have transfers. The remaining three all are up to 14 nights and have food and flights either included or to purchase. Calculate the price pppn of each holiday in GBP.

Step 2:

Divide by the number of nights to find the price per person per night

\text{Greece: }\pounds950 \div 7 = \pounds135.71\text{ pppn}

Multiply the price of food in euros by 1.27 to convert into GBP

\text{Spain: }\pounds105 + (30 \times 1.27) = \pounds143.10

Divide price per person by 7 to calculate the price per night. Flights must also be divide by 4 first to find the price per person.

\text{Portugal: }\dfrac{\pounds450}{7} + \dfrac{\pounds250}{4 \times 7} + 15 = \pounds88.21\checkmark