Question 1

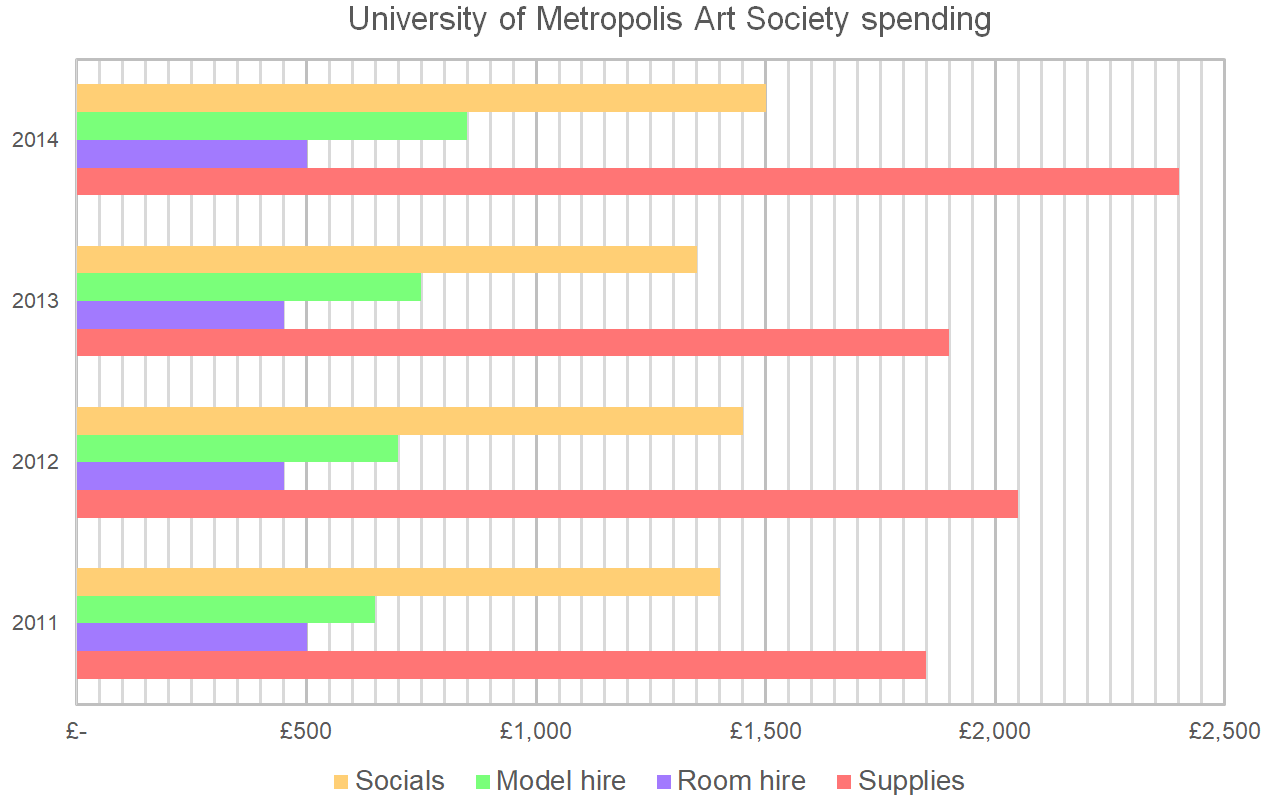
The total budget for the Art Society was £4,550 in 2011 and increased by 5% by 2012. In neither year did they spend their entire budgets. What is the ratio of the amount of money left unspent in 2011 compared to the amount of money left unspent in 2012?

A: 1.23 : 1

B: 1.18 : 1

C: 1.15 : 1

D: 1.04 : 1

Written Solutions

Step 1: Calculate the total budget for 2012.

A 5% increase corresponds to a multiplier of 1.05.

\text{2012 budget } = 4,550 \times 1.05 = \pounds 4,777.50

Step 2: Calculate the unspent money in both years.

2011: 4,550 - (1,400 + 650 + 500 + 1,850) = \pounds 150 \text{ left unspent.}

2012: 4,777.50 - (1,450 + 700 + 450 + 2,050) = \pounds 127.50 \text{ left unspent.}

Step 3: Form the ratio and simplify by dividing through by the smallest element.

\begin{aligned}\text{2011 unspent money : 2012 unspent money } &= \pounds 150 : \pounds 127.50 \\ &= \dfrac{150}{127.50} : \dfrac{127.50}{127.50} \\ &= 1.18 : 1 \end{aligned}

Question 2

From 2014 to 2015 the Art Society increased spending on supplies by 8%, model hire by 5%, and decreased spending on room hire by £80. Assuming the total spend remained the same, what was the percentage change in the spend on socials from 2014 to 2015?

A: 8.6%

B: 12.4%

C: 6.1%

D: 10.3%

Written Solutions

Step 1: Work out the money spent on supplies, model hire, and room hire in 2015.

An 8% increase corresponds to a multiplier of 1.08, and a 5% increase corresponds to a multiplier of 1.05. So, we get the following.

\text{2015 spend on supplies } = 2,400 \times 1.08 = \pounds 2,592

\text{2015 spend on model hire } = 850 \times 1.05 = \pounds 892.50

\text{2015 spend on room hire } = 500 - 80 = \pounds 420

Step 2: Calculate how much was spent on socials in 2015.

The total spend was the same as in 2014, so

\text{Total spend in 2015 } = 2,400 + 500 + 850 + 1,500 = \pounds 5,250

So, the \text{2015 spend on socials } = 5,250 - (2,592 + 892.50 + 420) = \pounds 1,345.50

Step 3: Determine the percentage change.

\dfrac{1,500 - 1345.50}{1,500} \times 100 = 10.3 \% \text{ decrease}.

Question 3

In 2013 the Art Society had 186 members. In 2014 they decided to increase the combined 2013 spend on supplies and socials by an amount equal to 20% of the total money they obtained from membership fees that year. Considering that membership costs £13 and must be renewed each year, by how much did the number of Art Society members increase from 2013 to 2014?

A: 64 members

B: 66 members

C: 68 members

D: 71 membersa

Written Solutions

Step 1: Work out the combined spend on supplies and socials for 2013 and 2014.

\text{2013 combined spend } = 1,900 + 1,350 = \pounds 3,250

\text{2014 combined spend } = 2,400 + 1,500 = \pounds 3,900

Step 2: Calculate how much was taken in from membership fees in 2014.

Firstly, \text{the difference in spend from 2013 to 2014 } = 3,900 - 3,250 = \pounds 650

Then, as this represents 20% of the total amount made from memberships, we can divide £650 by 0.20 to find the desired value.

650 \div 0.20 = \pounds 3,250 \text{ made from memberships in 2014}.

Step 3: Determine the difference in members from 2013 to 2014.

Membership costs £13, so we get:

\text{Number of members in 2014 } = 3,250 \div 13 = 250

Then, \text{2014 members - 2013 members } = 250 - 186 = 64

Question 4

Money spent on supplies is split between paints, paper, and canvases according the ratio 6: 4: 5. Calculate the decrease in spending on paints from 2012 to 2013 as a proportion of the total decrease in spending.

A: 28.6%

B: 30.0%

C: 30.7%

D: 35.9%

Written Solutions

Step 1: Calculate how much money was spent on paints in 2012 and 2013.

A ratio of 6:4:5 has 15 parts, and paints make up 6 of them, i.e. the amount of money spent on paint is equal to \frac{6}{15} multiplied by the total amount spent on supplies.

\text{2012 spend on paints } = \dfrac{6}{15} \times 2,050 = \pounds 820

\text{2013 spend on paints } = \dfrac{6}{15} \times 1,900 = \pounds 760

Step 2: Work out the decrease in spending on paints & the overall decrease in spending.

\text{Decrease in spending on paints } = 820 - 760 = \pounds 60

\text{Total spend in 2012 } = 2,050 + 450 + 700 + 1,450 = \pounds 4,650

\text{Total spend in 2013 } = 1,900 + 450 + 750 + 1,350 = \pounds 4,450

\text{Therefore, overall decrease } = 4,650 - 4,450 = \pounds 200

Step 3: Calculate the decrease in spending on paint as a proportion of the total decrease.

\dfrac{60}{200} \times 100 = 30 \%

Question 5

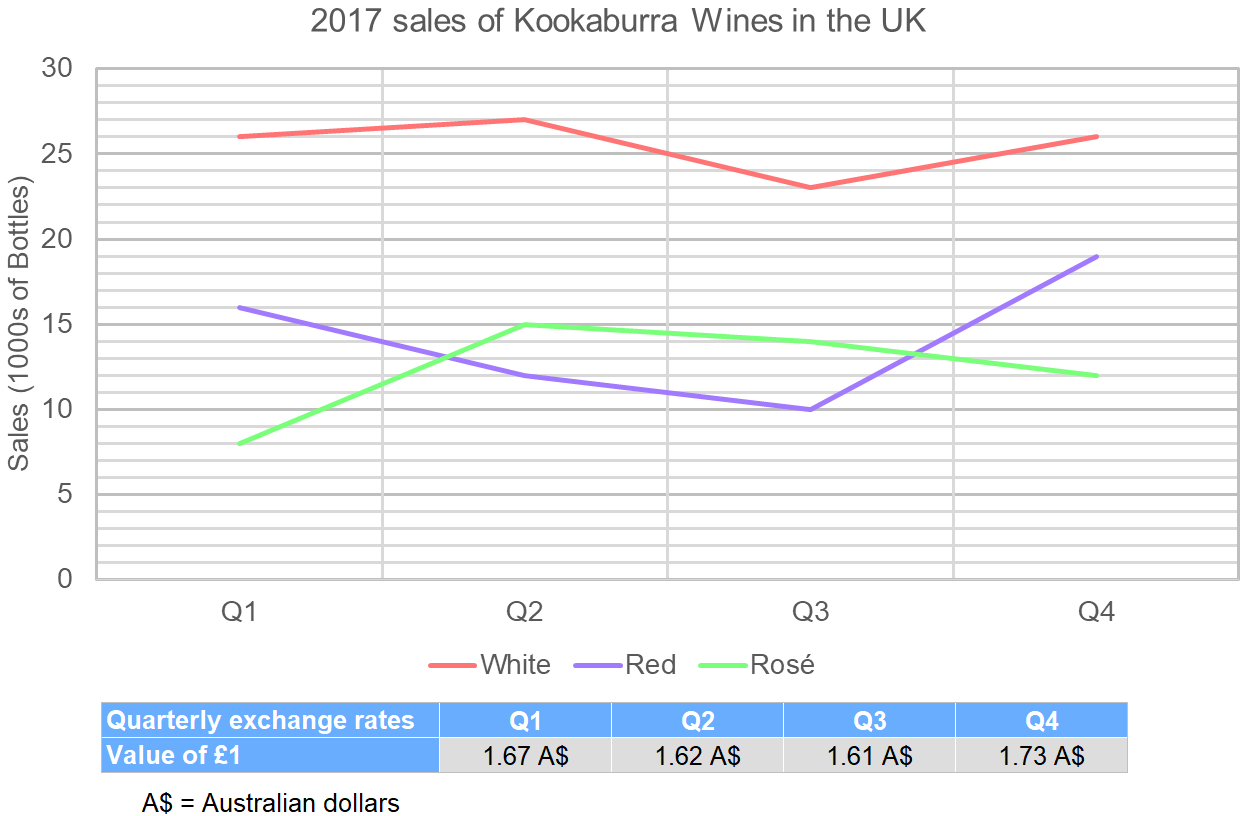
The profit made on red wine is £5.12 per bottle sold. Calculate, in Australian dollars, the profit on red wine sales in the fourth quarter as a proportion of the total yearly profit on red wine sales.

A: 29.6%

B: 31.2%

C: 35.2%

D: 40.1%

Written Solutions

Step 1: Calculate the profit in each quarter in pounds.

\text{Q1 profit } = 5.12 \times 16,000 = \pounds 76,800

\text{Q2 profit } = 5.12 \times 12,000 = \pounds 61,440

\text{Q3 profit } = 5.12 \times 10,000 = \pounds 51,200

\text{Q4 profit } = 5.12 \times 19,000 = \pounds 97,280

Step 2: Calculate the profit in each quarter in Australian dollars.

\text{Q1 profit } = 76,800 \times 1.67 = 128,256 \text{ A}\$

\text{Q2 profit } = 61,440 \times 1.62 = 99,532.80 \text{ A}\$

\text{Q3 profit } = 51,200 \times 1.61 = 82,432 \text{ A}\$

\text{Q4 profit } = 97,280 \times 1.73 = 168,294.40 \text{ A}\$

Step 3: Work out the Q4 profit as a proportion.

\text{Total yearly profit } = 128,256 + 99,532.80 + 82,432 + 168,294.40 = 478,515.2 \text{ A}\$

\begin{aligned} &\dfrac{\text{Q4 profit}}{\text{Total yearly profit}} \\ = &\dfrac{168,294.40}{478,515.2} \times 100 = 35.2 \% \end{aligned}

Question 6

A bottle of red wine requires 24% more grapes to produce than a bottle of white wine. Given that the total number of grapes used to make white wine in the first and second quarter was 34,450,000, work out the difference between the number of grapes needed for red wine in Q1 and the number of grapes needed for white wine in Q3.

A: 1,598,000 grapes

B: 1,806,000 grapes

C: 2,054,000 grapes

D: 2,153,000 grapes

Written Solutions

Step 1: Determine how many grapes are needed for a single bottle of white wine.

34,450,000 \div (26,000 + 27,000) = 650 \text{ grapes per bottle of white}

Step 2: Work out how many grapes are needed for a bottle of red wine.

A 24% increase corresponds to a multiplier of 1.24.

650 \times 1.24 = 806 \text{ grapes per bottle of red}

Step 3: Calculate the difference stated in the question.

\text{Number of grapes for red wine in Q1 } = 806 \times 16,000 = 12,896,000

\text{Number of grapes for white win in Q3 } = 650 \times 23,000 = 14,950,000

\text{Difference } = 14,950,000 - 12,896,000 = 2,054,000 \text{ grapes}

Question 7

A restaurant owner buys white wine & rosé from Kookaburra Wines in the ratio 5: 2. She purchased 1,080 bottles of rosé in each quarter of 2017. If she stopped buying produce from Kookaburra Wines at the end of the second quarter, what would’ve been the percentage decrease in sales of bottles of wine from Q2 to Q3?

A: 30.5%

B: 20.0%

C: 26.7%

D: 23.8%

Written Solutions

Step 1: Work out how much wine she purchased in each quarter.

The ratio is 5:2, so there are 7 parts. The 1,080 bottles of rosé constitute 2 of these parts, therefore \text{1 part } = 1,080 \div 2 = 540. So, we get:

\text{Wine purchased per quarter } = 540 \times 7 = 3,780 \text{ bottles}

Step 2: Calculate the total sales for Q3 without her purchases.

\text{Q3 total } = 23,000 + 10,000 + 14,000 = 47,000 \text{ bottles}

\text{Therefore, new total } = 47,000 - 3,780 = 43,220 \text{ bottles}

Step 3: Calculate, using this new total, the percentage decrease.

\text{Q2 total } = 27,000 + 12,000 + 15,000 = 54,000 \text{ bottles}

\dfrac{54,000 - 43,220}{54,000} \times 100 = 20.0 \%

Question 8

Halfway through the year the cost of a bottle of rosé was upped by 30% to £16.38. Work out the ratio of sales, in A$, of rosé in Q1 compared to Q2 and Q3.

A: 1: 1.72 : 2.22

B: 1 : 1.82 : 2.19

C: 1 : 1.76 : 1.99

D: 1 : 1.54 : 1.98

Written Solutions

Step 1: Calculate the cost of a bottle of rosé in the first half of the year.

A 30% increase corresponds to a multiplier of 1.30. The original value must have been multiplied by 1.3 to obtain the new price of £16.38, so to find the previous value we must divide by 1.3.

\text{Cost in first half of year } = 16.38 \div 1.3 = \pounds 12.60

Step 2: Calculate the revenue on sales of rosé for Q1, Q2, and Q3 in pounds.

\text{Q1 rosé sales } = 12.60 \times 8,000 = \pounds 100,800

\text{Q2 rosé sales } = 12.60 \times 15,000 = \pounds 189,000

\text{Q3 rosé sales } = 16.38 \times 14,000 = \pounds 229,320

Step 3: Convert to A$.

\text{Q1 rosé sales } = 1.67 \times 100,800 = 168,336 \text{ A}\$

\text{Q2 rosé sales } = 1.62 \times 189,000 = 306,180 \text{ A}\$

\text{Q3 rosé sales } = 1.61 \times 229,320 = 369,205.20 \text{ A}\$

Step 4: Form the ratio and simplify by dividing through by the smallest element.

\begin{aligned}\text{Q1 rosé sales : Q2 rosé sales : Q3 rosé sales } &= 168,336:306,180:369,205.20 \\ &= \dfrac{168,336}{168,336} : \dfrac{306,180}{168,336} : \dfrac{369,205.20}{168,336} \\ &= 1 : 1.82 : 2.19 \end{aligned}

Question 9

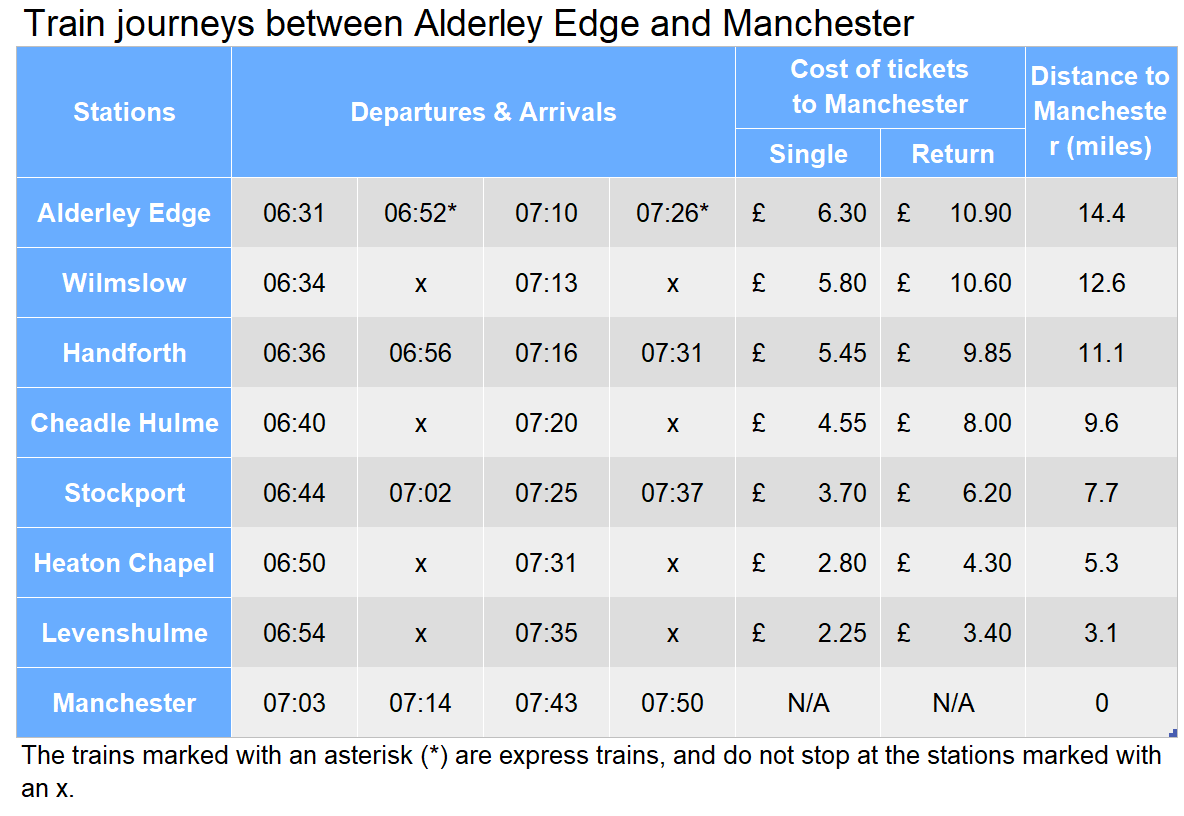
Calculate the highest average speed travelled between stops for the train departing Alderley Edge at 07:26.

A: 39.6 mph

B: 41.2 mph

C: 44.0 mph

D: 35.5 mph

Written Solutions

Step 1: Work out the distances between each of the four stops.

\text{Alderley Edge to Handforth } = 14.4 - 11.1 = 3.3 \text{ miles}

\text{Handforth to Stockport } = 11.1 - 7.7 = 3.4 \text{ miles}

\text{Stockport to Manchester } = 7.7 \text{ miles}

Step 2: Find the time taken for each portion of the journey in hours.

\text{Alderley Edge to Handforth = 5 minutes, or } 5 \div 60 = \frac{1}{12} \text{ hours}

\text{Handforth to Stockport = 6 minutes, or } 6 \div 60 = \frac{1}{10} \text{ hours}

\text{Stockport to Manchester = 13 minutes, or } 13\div 60 = \frac{13}{60} \text{ hours}

Step 3: Calculate the average speed for each portion of the journey.

\text{Alderley Edge to Handforth speed } = 3.3 \div \frac{1}{12} = 39.6 \text{ mph}

\text{Handforth to Stockport speed } = 3.4 \div \frac{1}{10} = 34 \text{ mph}

\text{Stockport to Manchester speed } = 7.7 \div \frac{13}{60} = 35.5 \text{ mph}

The fastest speed is 39.6 mph.

Question 10

A school trip of 5 teachers and 46 students is going from Handforth to Manchester for a day trip. Trains leaving after 7am offer a 20% reduction on the cost of any ticket for students. Assuming all people on the trip require return tickets, work out the ratio for the total cost of the tickets for the 06:56 departure compared to the total cost of all the tickets for the 07:10 departure.

A: 1.18 : 1

B: 1.20 : 1

C: 1.22 : 1

D: 1.24 : 1

Written Solutions

Step 1: Work out the cost of tickets for the 06:56 departure.

There are a total of 5 + 46 = 51 return tickets required, and they all cost the same amount of £9.85.

\text{So, the total cost } = 51 \times 9.85 = \pounds 502.35

Step 2: Work out the cost of tickets for the 07:16 departure.

There is a 20% reduction on the cost of all 46 student tickets. This corresponds to a multiplier of 0.8.

\text{New cost of student ticket } = 9.85 \times 0.8 = \pounds 7.88

\text{So, total cost } = (46 \times 7.88) + (5 \times 9.85) = 362.48 + 49.25 = \pounds 411.73

Step 3: Form the ratio and simplify by dividing through by the smallest element.

\begin{aligned} \text{06:56 departure cost : 07:16 departure cost } &= 502.35 : 411.73 \\ &= \dfrac{502.35}{411.73} : \dfrac{411.73}{411.73} \\ &= 1.22 : 1 \end{aligned}

Question 11

Every weekday, a man gets a taxi costing £3.10 to Cheadle Hulme station to then buy a return train ticket to Manchester. After doing this journey 165 times, he realised that a taxi to Stockport station would only cost him £0.50 more. Work out the percentage reduction in cost if he chooses to go to Manchester via Stockport station for the remainder of the year rather than stick with his current route. Assume 48 working weeks in a year.

A: 3.4%

B: 4.1%

C: 5.4%

D: 2.9%

Written Solutions

Step 1: Calculate the cost of taking his original journey for a whole year.

In one year he makes his journey 48 \times 5 = 240 times.

\text{Total cost of journey } = 3.10 + 8.00 = \pounds 11.10

\text{Total cost for the year } = 240 \times 11.10 = \pounds 2,664

Step 2: Calculate the cost of switching up his journey after the first 165 days.

\text{Cost for first 165 days } = 11.10 \times 165 = \pounds 1831.50

The number of days left on which he’ll travel is 240 - 165 = 75.

\text{Cost of new journey } = 3.10 + 0.50 + 6.20 = \pounds 9.80

\text{Cost for last 75 days } = 75 \times 9.80 = \pounds 736

\text{So, total cost for the year } = 736 + 1,831.50 = \pounds 2,567.50

Step 3: Work out the percentage decrease in cost.

\dfrac{2,664 - 2,567.50}{2,664} \times 100 = 2.9 \%

Question 12

On average, a non-express train picks up 8 people per station whilst an express train picks up 14. Additionally, the entire running costs for an express train are £4.96 per minute of travel, a 20% reduction on the cost per minute for a standard train. Considering this, what is the decrease in profit on the longest journey from Alderley Edge compared to the shortest? Assume all tickets are singles.

A: £64.98

B: £57.62

C: £55.04

D: £46.32

Written Solutions

Step 1: Determine which journeys are shortest and longest by subtracting departure time from arrival time.

06:31 departure: 07:03 - 06:31 = 00:32

06:52 departure: 07:14 - 06:52 = 00:22 – shortest.

07:10 departure: 07:43 - 07:10 = 00:33 – longest.

07:26 departure: 07:50 - 07:26 = 00:24

Step 2: Work out money made from tickets on both journeys.

Shortest journey is an express train, so 14 people buy singles at each stop. Therefore, we get:

\text{Money made } = 14 \times (6.30 + 5.45 + 3.70) = \pounds 216.30

Longest journey is a non-express train, so 8 people buy singles at each stop. Therefore, we get:

\text{Money made } = 8 \times (6.30 + 5.80 + 5.45 + 4.55 + 3.70 + 2.80 + 2.25) = \pounds 246.80

Step 3: Work out running costs of both journeys.

£4.96 is a 20% reduction on the cost for a non-express train. This corresponds to a multiplier of 0.8 being multiplied by the original cost to obtain 4.96, so we must divide by 0.8 to find the value.

4.96 \div 0.8 = \pounds 6.20.

\text{Shortest journey cost } = 22 \times 4.96 = \pounds 109.12

\text{Longest journey cost } = 33 \times 6.20 = \pounds 204.60

Step 4: Subtract the profit made on the longest journey from that of the shortest.

\begin{aligned}&\text{Shortest journey profit - longest journey profit } \\ = &(216.30 - 109.12) - (246.80 - 204.60) \\ = & \pounds 64.98\end{aligned}

Question 13

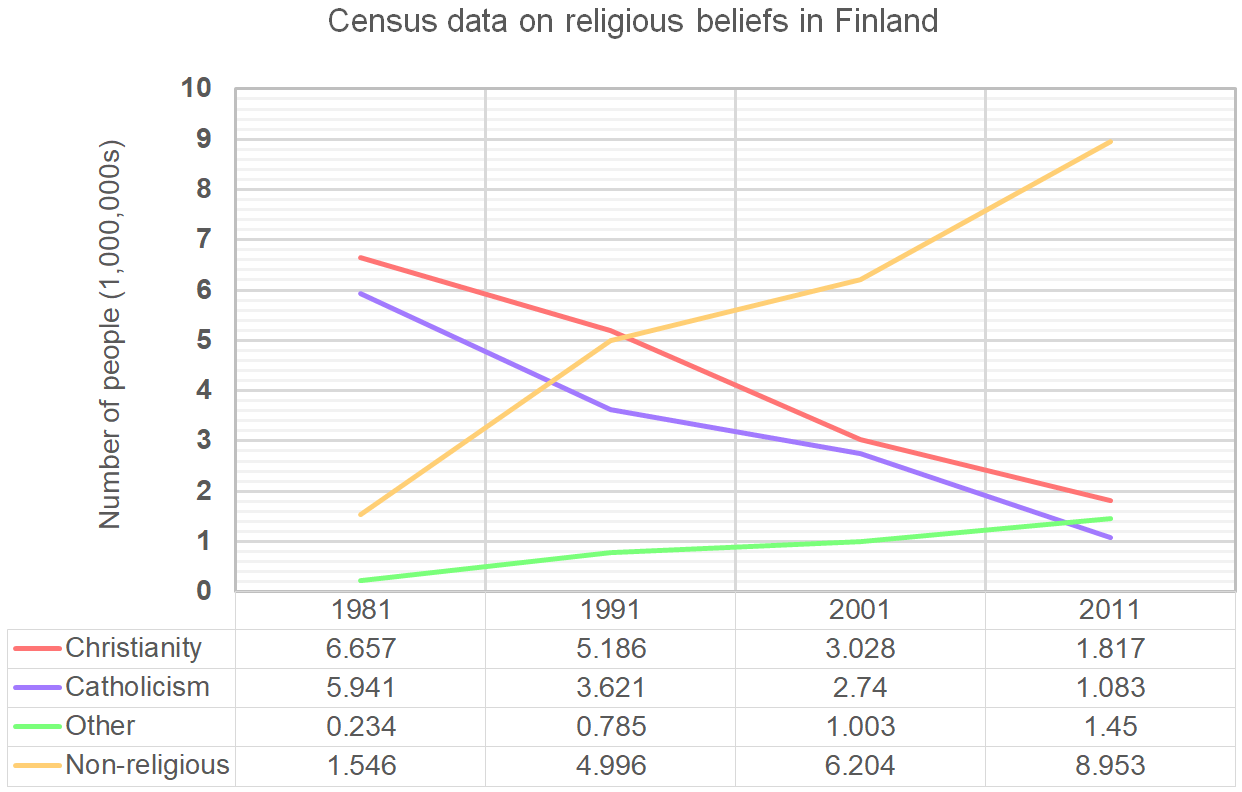
In 1995, they decided to make the question of religious beliefs non-compulsory. Assuming a 2% growth in adult population every 5 years after 1991, what percentage of the adult population chose not to answer the census question on religious beliefs in 2011?

A: 12.8%

B: 13.9%

C: 14.9%

D: 15.8%

Written Solutions

Step 1: Calculate the total population in 2011.

NOTE: for ease, we can keep all values in the decimal form listed in the table rather than multiplying them all by 1 million. As a percentage has no units, this will not affect the final calculation.

\text{Total population in 1991 } = 5.186 + 3.621 + 0.785 + 4.996 = 14.588 \text{ million}

A 2% increase corresponds to a multiplier of 1.02. We will have to apply this multiplier 4 times, as 20 years passed between 1991 and 2011.

\text{Total population in 2001 } = 14.588 \times 1.02^4 = 15.790520 \text{ million}

Step 2: Work out how many people didn’t answer the question on religious beliefs in 2011.

\text{Total recorded answers } = 1.817 + 1.083 + 1.45 + 8.953 = 13.303 \text{ million}

\text{Number who abstained } = 15.790520 - 13.303 = 2.487520 \text{ million}.

Step 3: Determine the amount as a percentage of the whole population in 2011.

\dfrac{2.487520}{15.790520} \times 100 = 15.8 \%

Question 14

In 1981, 46% of 18-24-year-olds answered “non-religious”, and by 1991 this value was 75%. In both years, the non-religious category was split between the age ranges 18-24, 25-39, and 40+ according to the ratio 5: 2: 1. What is the ratio of the number of 18-24-year-olds living in Finland in 1981 compared to 1991?

A: 1: 2.05

B: 1 : 1.98

C: 1 : 1.88

D: 1 : 1.73

Written Solutions

Step 1: Work out how many 18-24-year-olds answered non-religious in 1981 and 1991.

NOTE: for ease, we can keep all values in the decimal form listed in the table rather than multiplying them all by 1 million. As we’re forming a ratio, it won’t affect the final answer.

The ages are split according to the ratio 5:2:1, which means that 18-24-year-olds make up \dfrac{5}{5+2+1} = \dfrac{5}{8} of the people who answered non-religious.

The amounts of people who answered non-religious are as follows.

1981: \dfrac{5}{8} \times 1.546 = 0.96625 \text{ million}

1991: \dfrac{5}{8} \times 4.996 = 3.1225 \text{ million}

Step 2: Work out how many 18-24-year-olds lived in Finland in 1981 and 1991.

In 1981, the amount who answered non-religious constituted 46% of the total, so if we then divide the amount calculated above by 0.46 we can find the total. The same goes for 1991, except then we should divide the other amount by 0.75 to receive the total for that year.

1981: 0.96625 \div 0.46 = 2.100543 \text{ million}

1991: 3.1225 \div 0.75 = 4.163333 \text{ million}

Step 3: Form the ratio and simplify by dividing through by the smallest element.

\begin{aligned} \text{18-24-year-olds in 1981 : 18-24-year-olds in 1991 } &= 2.100543 : 4.163333 \\ &= \dfrac{2.100543}{2.100543} : \dfrac{4.163333}{2.100543} \\ &= 1 : 1.98 \end{aligned}

Question 15

People who identified as Christian or Catholic visit their places of worship an average of 0.8 times per week, whilst those in the “other” category visit theirs an average of 6.2 times per month. What was the percentage decrease in the number of annual visits to places of worship from 1981 to 1991?

A: 27.9%

B: 23.5%

C: 21.6%

D: 20.4%

Written Solutions

Step 1: Calculate the total number of annual visits for 1981.

NOTE: for ease, we can keep all values in the decimal form listed in the table rather than multiplying them all by 1 million. As a percentage has no units, this will not affect the final calculation.

Christianity and Catholicism:

\text{Number of weekly visits in 1981 } = 0.8 \times (6.657 + 5.941) = 10.0784

Other religions:

\text{Number of monthly visits in 1981 } = 6.2 \times 0.234 = 1.4508

Now, we must multiply these numbers by 52 and 12 respectively and sum the answers to determine the annual visit numbers.

\text{Total visits in 1981 } = (52 \times 10.0784) + (12 \times 1.4508) = 541.8464

Step 2: Calculate the total number of annual visits for 1991.

Christianity and Catholicism:

\text{Number of weekly visits in 1991 } = 0.8 \times (5.186 + 3.621) = 7.0456

Other religions:

\text{Number of monthly visits in 1991 } = 6.2 \times 0.785 = 4.867

Now, we must multiply these numbers by 52 and 12 respectively and sum the answers to determine the annual visit numbers.

\text{Total visits in 1991 } = (52 \times 7.0456) + (12 \times 4.867) = 424.7752

Step 3: Determine the percentage decrease.

\dfrac{541.8464 - 424.7752}{541.8464} \times 100 = 21.6 \% \text{ decrease}

Question 16

It is predicted that the total number of religious people in Finland will continue to decrease from 2011 to 2021 at the same percentage rate it did from 2001 to 2011. If the total number of people who answered the census question remains the same, what percentage of people does this model predict will be non-religious in 2021?
A: 86.0%

B: 87.1%

C: 84.6%

D: 83.7%

Written Solutions

Step 1: Calculate the percentage rate of decrease in number of religious people from 2001 to 2011.

\text{2001 total } = 3.028 + 2.74 + 1.003 = 6.771 \text{ million}.

\text{2011 total } = 1.187 + 1.083 + 1.45 = 3.72 \text{ million}

\text{Percentage decrease } = \dfrac{6.771 - 3.72}{6.771} \times 100 = 45.06 \%

Step 2: Find the number of people who the model predicts will identify as religious in 2021.

A 45.1% decrease corresponds to a multiplier of 0.549.

3.72 \times 0.5494 = 2.04228 \text{ million religious people in 2021}

Step 3: Calculate the number who will identify as non-religious in 2021 as a percentage.

The total who answered the census questions remains the same, so

\text{2021 total } = 1.817 + 1.083 + 1.45 + 8.953 = 13.303 \text{ million}

\text{Non-religious percentage } = \dfrac{13.303 - 2.04228}{13.303} \times 100 = 84.6 \%

Question 17

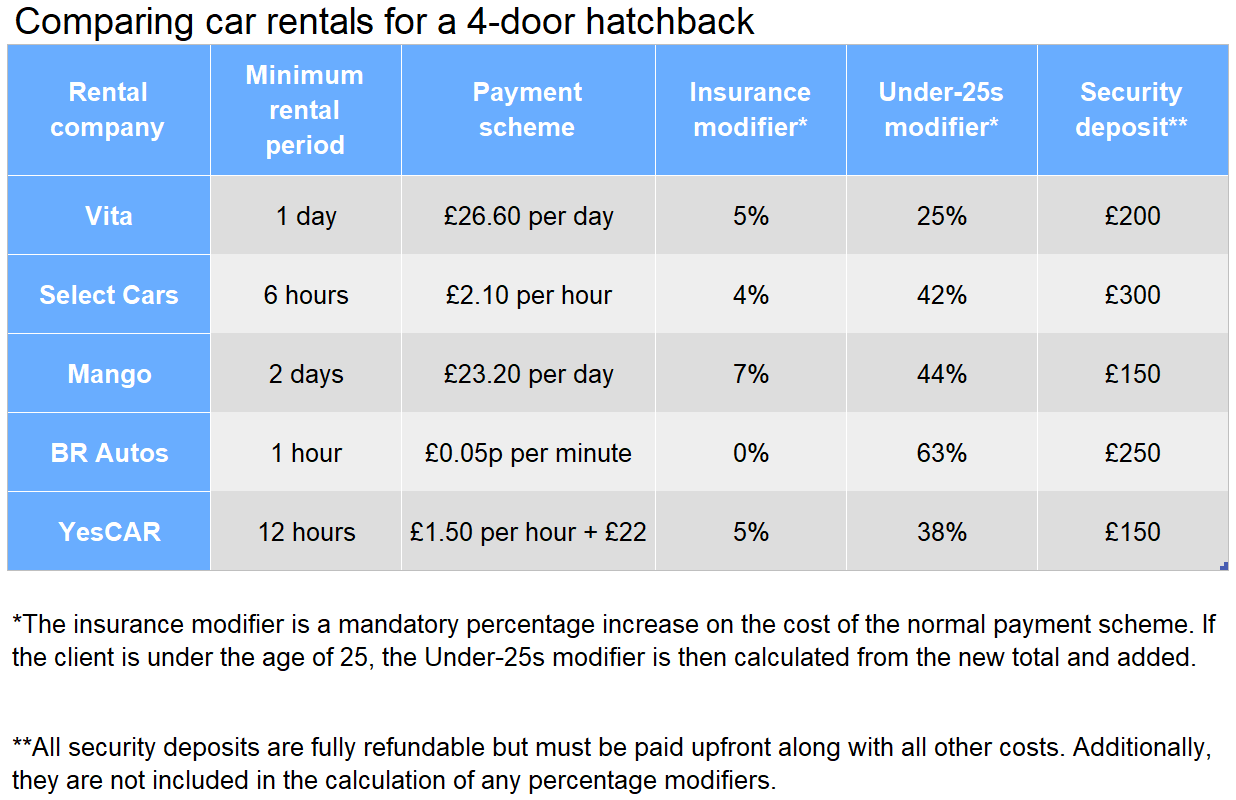
Work out the ratio of the upfront cost for a 38-year-old renting a car for 36 hours with Vita compared to YesCAR.

A: 1.05 : 1

B: 1.11 : 1

C: 1 : 1.05

D: 1: 1.11

Written Solutions

Step 1: Determine the upfront cost of renting with Vita for 36 hours.

The payment scheme for Vita would require you to pay for 2 days, which will cost

26.60 \times 2 = \pounds 53.20

Furthermore, a 5% insurance modifier corresponds to a multiplier of 1.05. So, the cost becomes:

53.20 \times 1.05 = \pounds 55.86.

\text{Therefore, total cost } = 55.86 + 200 = \pounds 255.86

Step 2: Determine the upfront cost of renting with YesCAR for 36 hours.

A 36-hour rental with YesCAR will cost

(36 \times 1.50) + 22 = \pounds 76.

Furthermore, a 5% insurance modifier corresponds to a multiplier of 1.05. So, the cost becomes:

76 \times 1.05 = \pounds 79.80

\text{Therefore, total cost } = 150 + 79.80 = \pounds 229.80

Step 3: Form the ratio and simplify by dividing through by the smallest element.

\begin{aligned}\text{Vita cost : YesCAR cost} &= 255.86 : 229.80 \\ &= \dfrac{255.86}{229.80} : \dfrac{229.80}{229.80} \\ &= 1.11 : 1\end{aligned}

Question 18

Select Cars rented out this car 225 times in one year, for an average of 10 hours at a time. On 32 occasions the client was under 25. On 8% of occasions, deposit money received by Select Cars is retained with good reason, however, Select Cars have been accused of unjustly retaining client’s entire security deposits in 4% of all possible cases. If this is true, what percentage has their revenue from renting this car increased because of the scam?

A: 20.3%

B: 24.3%

C: 25.7%

D: 27.0%

Written Solutions

Step 1: Calculate the revenue made (fairly) from the over-25s.

10 hours with Select Cars means the base cost is 10 \times 2.10 = \pounds 21.

The insurance modifier of 4% corresponds to a multiplier of 1.04, so the cost increases as such:

21 \times 1.04 = \pounds 21.84

Furthermore, 8% of the deposit money would equate to 0.08 \times 300 = \pounds 24 per rental.

There were 225 - 32 = 193 over-25s, so the total revenue is

193 \times (21.84 + 24) = \pounds 8,847.12

Step 2: Calculate the revenue made (fairly) from the under-25s.

The base cost plus insurance modifier would remain the same at £21.84. Then, the under-25s modifier of 42% corresponds to a multiplier of 1.42, so we get the following increased cost.

21.84 \times 1.42 = \pounds 31.01

The 8% of the deposit money remains the same, so the total is:

32 \times (31.01 + 24) = \pounds 1,760.32

Step 3: Determine the money made from the scam as a percentage of the whole revenue.

4% of 225 is 225 \times 0.04 = 9 people.

\text{Total money unjustly retained } = 9 \times 300 = 2,700

As a percentage of the total:

\dfrac{2,700}{2,700 + 1,760.32 + 8,847.12} \times 100 = 20.3 \%

Question 19

A 22-year-old woman wishes to rent a car for 7 hours and no more. Work out the difference between the actual cost per hour, with all upfront costs considered, between her two options.

A: £5.36

B: £4.42

C: £4.21

D: £3.96

Written Solutions

Step 1: Her two options are clearly Select Cars and BR Autos. Work out the cost of renting with Select Cars.

\text{Base cost } = 2.10 \times 7 = \pounds 14.70

The insurance modifier of 4% corresponds to a multiplier of 1.04, so we get the following increase:

14.70 \times 1.04 = \pounds 15.29

The under-25s modifier of 42% corresponds to a multiplier of 1.42, so we get the increased value:

15.29 \times 1.42 = \pounds 21.71

\text{Total cost } = 21.71 + 300 = \pounds 321.71

Step 2: Work out the cost of renting with BR Autos.

7 hours is equal to 7 \times 60 = 420 minutes.

\text{Base cost } = 0.05 \times 420 = \pounds 21.

There is no insurance modifier. So, we go straight to the under-25s modifier of 63%, which corresponds to a multiplier of 1.63. This gives us the increase value:

21 \times 1.63 = 34.23

\text{Total cost } = 34.23 + 250 = \pounds 284.23

Step 3: Determine the difference between the actual hourly costs.

\text{Select Cars hourly cost } = 321.71 \div 7 = \pounds 45.96

\text{BR Autos hourly cost } = 284.23 \div 7 = \pounds 40.60

\text{Difference } = 45.96 - 40.60 = \pounds 5.36

Question 20

What is the minimum number of hours 24-year-old woman would have to rent a car from BR Autos for her upfront costs to exceed those of a 40-year-old man renting a car from Mango for a week?

A: 16 hours

B: 27 hours

C: 39 hours

D: 55 hours

Written Solutions

Step 1: Calculate the cost of a 40-year-old man renting a car with Mango for a week.

\text{Base cost } = 7 \times 23.20 = \pounds 162.40

The insurance modifier of 7% corresponds to a multiplier of 1.07.

\text{Cost with insurance } = 162.40 \times 1.07 = \pounds 173.77

\text{Total cost } = 173.77 + 150 = \pounds 323.77

Step 2: Determine the cost per hour for a 24-year-old woman renting with BR Autos, with all the modifiers added.

\text{Base cost } = 0.05 \times 60 = \pounds 3 \text{ per hour}

There is no insurance modifier. The under-25s modifier corresponds to a multiplier of 1.63.

\text{Cost with modifier } = 3 \times 1.63 = \pounds 4.89 \text{ per hour}

Step 3: Calculate the number of hours, as stated in the question.

We require the cost of the BR Autos rental to be greater than £323.77. We know that regardless of length of rental, BR Autos will charge £250 for a security deposit, which means that the cost which comes from the payment scheme (plus modifiers), i.e. not the deposit, must exceed

323.77 - 250 = \pounds 73.77

As we determined that the cost per hour for BR Autos was £4.89, the number of hours it would take for the cost to be equal to that of Mango’s is

73.77 \div 4.89 = 15.1 \text{ hours}

So, to exceed the cost of renting with Mango for a week, it must be rented for a minimum of 16 hours.