Question 1

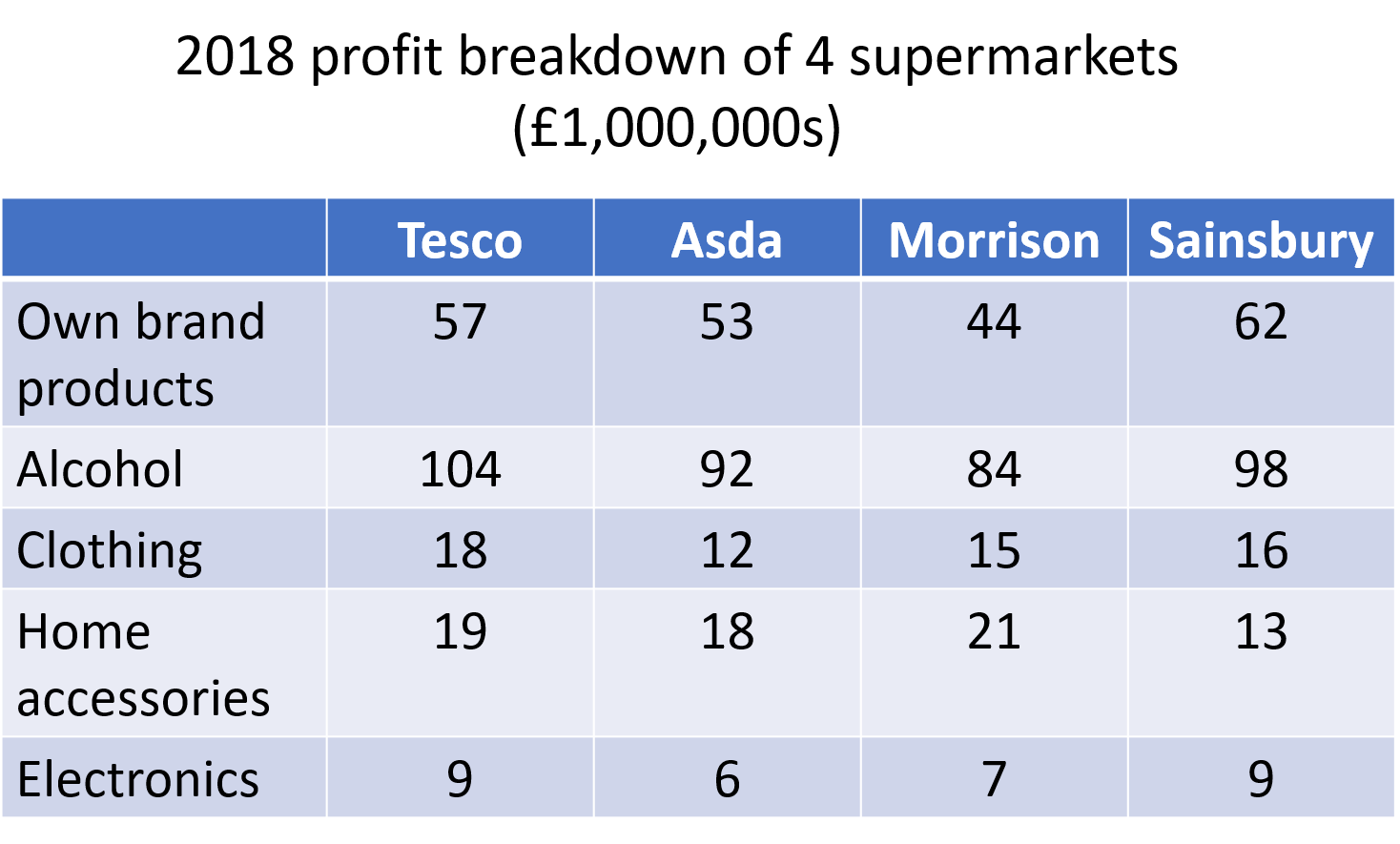
Which supermarket made the greatest percentage of their revenue from alcohol sales?

A: Tesco

B: Asda

C: Morrison

D: Sainsbury

Written Solutions

Tesco’s total revenue was £57 + £104 + £18 + £19 + £9 = \pounds207 (million). Alcohol sales were \pounds104 (million).
The percentage of the alcohol sales was:

104 \div 207 \times 100 = 50.24\%

Asda’s total revenue was £53 + £92 + £12 + £18 + £6 = \pounds181 (million). Alcohol sales were \pounds92 (million).
The percentage of the alcohol sales was:

92 \div 181 \times 100 = 50.82%\

Morrison’s total revenue was £44 + £84 + £15 + £21 + £7 = \pounds171 (million). Alcohol sales were \pounds84 (million).

The percentage of the alcohol sales was:

84 \div 171 \times 100 = 49.12\%

Sainsbury’s total revenue was £62 + £98 + £16 + £13 + £9 = \pounds198 (million). Alcohol sales were \pounds98 (million). The percentage of the alcohol sales was:

98 \div 198 \times 100 = 49.49\%

Therefore Asda made the greatest percentage of their revenue from alcohol sales.

Question 2

Tesco’s revenue came from cash purchases and card payments in the ratio of 2 : 7.  How much revenue came from Amex payments if 1/7 of card payments were made by Amex?

A: £23 million

B: £26 million

C: £29 million

D: £32 million

Written Solutions

Tesco’s total revenue was \pounds207 million. If cash purchases and card payments were in the ratio of 2 : 7, then card payments accounted for \frac{7}{9} of all transactions (we are dealing with ninths because the sum of the ratio is 9).

We can now work out the value of all the card transactions:

\pounds207 (million) \times \frac{7}{9} = \pounds161 ( million

If \frac{1}{7} of the \pounds161 million was from Amex payments, we can easily work this out:

\pounds161 million \times \frac{1}{7} = \pounds23 million

or

\pounds161 million \div 7 = \pounds23 million

Question 3

Morrison’s total revenue increased by 15% the following year and alcohol sales comprised 38% of annual revenue.  To the nearest million, what was the difference in sales of alcohol between 2018 and 2019?

A: £4 million

B: £8 million

C: £9 million

D: £12 million

Written Solutions

Morrison’s total revenue was \pounds171 million. If their sales increased by 15\%, then the following year they would have made:

1.15 \times \pounds171 \text{ million} = \pounds196.65 \text{ million}

If alcohol comprised 38\% of this amount, then the value of the total alcohol sales was:

0.38 \times \pounds196.65 \text{ million} = \pounds74.727 \text{ million}

The previous year, Morrison’s alcohol sales came to a total of \pounds84 million, therefore the difference was:

\pounds84 - \pounds74.727 = \pounds9.273 \text{ million, so} \pounds9 million to the nearest million.

Question 4

Asda’s clothing sales increase by 20% in 2019 with men’s clothing and women’s clothing being sold in the ratio of 2 : 3.  If the average spend on women’s clothing in 2019 was £34.99, how many women’s clothing transactions took place in 2019 to the nearest fifty million?

A: 150 million

B: 200 million

C: 250 million

D: 300 million

Written Solutions

Asda’s clothing was \pounds12 million. If it increased by 20\%, then the new value would be:

\pounds12 \text{ million} \times 1.2 = \pounds14.4 million

If men’s clothing and women’s clothing was sold in the ratio of 2 : 3, this means that women’s clothing accounted for \frac{3}{5} of the total (we are dealing in fifths because the sum of the ratio is 5). Therefore the total value of women’s clothing sales was:

\pounds14.4 million \times \frac{3}{5} = \pounds8.64 million

If the average spend was \pounds34.99, then the number of women’s clothing transaction can be calculated as follows:

\pounds8.64 million \div \pounds34.99 = 246,927 million

To the nearest fifty million, this would be 250,000 million transactions.

Question 5

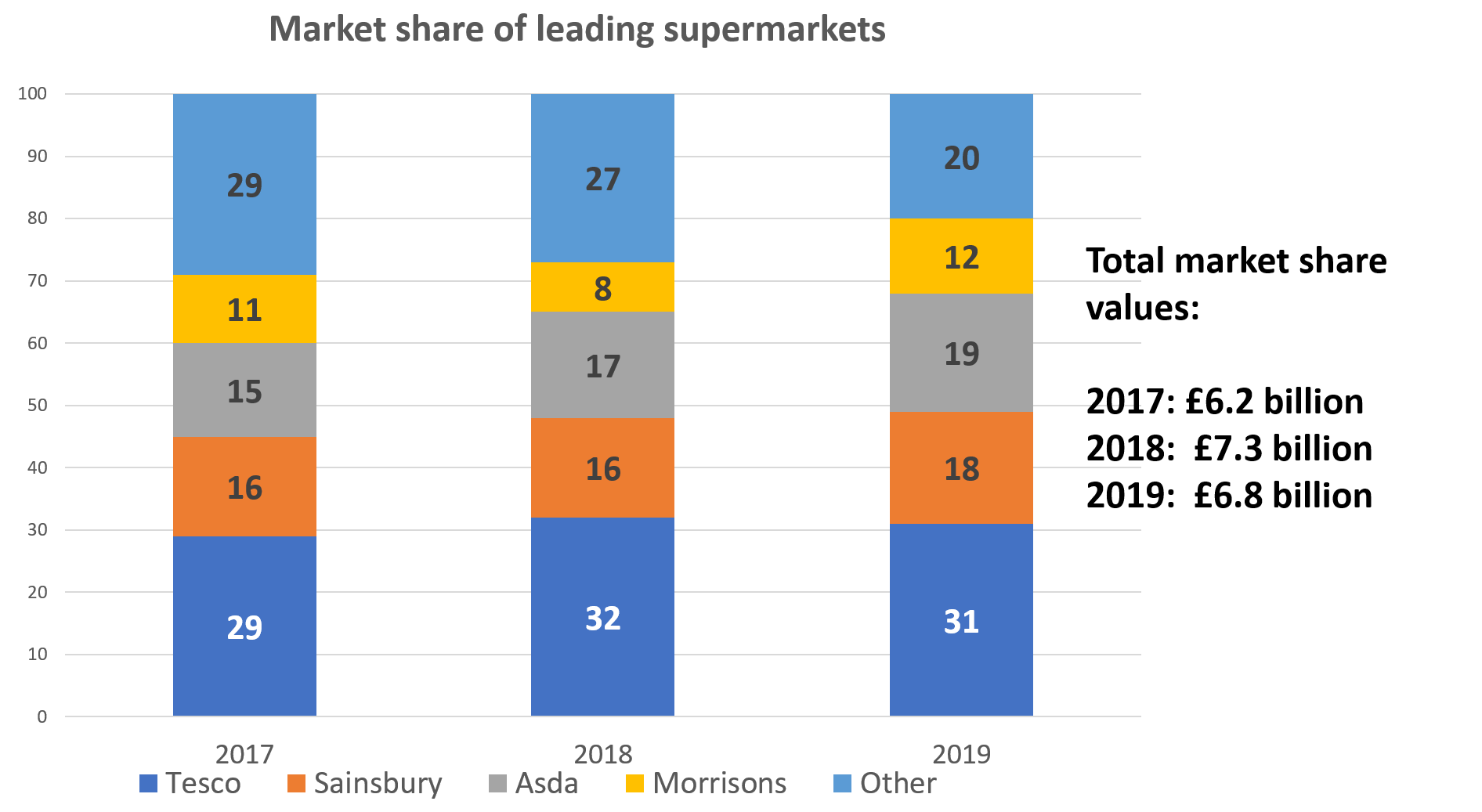
In 2018, what was the value of Morrison’s market share?

A: £48,600,000

B: £584,000,000

C: £486,000,000

D: £5,840,000,000

Written Solutions

In 2018, the total market share was \pounds7.3 billion. Morrison’s accounted for 8\% of this, so the value of their market share can be calculated as follows:

\pounds7.3 \text{ billion} \times 0.08 = \pounds0.584 billion

\pounds0.584 \text{ billion} \times 1,000,000,000 = \pounds584,000,000

Question 6

What was the mean value of the market share of Sainsbury’s over the 3 year period?

A: £777,600,000

B: £865,800,050

C: £1,128,000,000

D: £1,224,000,000

Written Solutions

In 2017, the total market share was \pounds6.2 billion. Sainsbury’s market share was 16\%, so their market share had a value of:

\pounds6.2 \text{ billion} \times 0.16 = \pounds0.992 billion

In 2018, the total market share was \pounds7.3 billion. Sainsbury’s market share was 16\%, so their market share had a value of:

\pounds7.3 \text{ billion}\times 0.16 = \pounds1.168 billion

In 2019, the total market share was \pounds6.8 billion. Sainsbury’s market share was 18\%, so their market share had a value of:

\pounds6.8 \text{ billion} \times 0.18 = \pounds1.224 billion

Therefore, the mean value of their market share was:

\dfrac{\pounds0.992 \text{ billion} + \pounds1.168 \text{ billion} + \pounds1.224 \text{ billion}}{3} = \pounds1.128 billion

\pounds1.128 \text{ billion} \times 1,000,000,000 = \pounds1,128,000,000

Question 7

What was the revenue of the Co-op in 2019 if it comprised ¾ of the ‘Other’ category?

A: £0.84 billion

B: £968,000,000

C: £1.02 billion

D: £1.36 billion

Written Solutions

In 2019, the total market share was \pounds6.8 billion and the ‘Other’ category accounted for 20\% of this. Therefore, the value of the ‘Other’ category was:

\pounds6.8 \text{ billion} \times 0.2 = \pounds1.36 billion

If the Co-op accounted for \frac{3}{4} of this, then their market share was worth:

1.36 \times \frac{3}{4} = \pounds1.02 billion

Question 8

The projected total market share in 2020 is £7.5 billion.  Morrison’s are aiming to increase their market share to 16%.  How much more revenue will they generate compared to 2019 if they hit this target?

A: £28,000,000

B: £280,000,000

C: £384,000,000

D: £466,000,000

Written Solutions

In 2019, Morrison’s market share was 12\% of the total market share of \pounds6.8 billion, so their market share was worth:

\pounds6.8 \text{ billion} \times 0.12 = \pounds0.816 billion

If the total market share in 2020 is expected to be £7.5 billion and Morrison’s are looking to have 16% of it, then, if they succeed, their market share will be worth:

\pounds7.5 \text{ billion} \times 0.16 = \pounds1.2 billion

This would be a difference of:

\pounds1.2 \text{ billion} - \pounds0.816 \text{ billion} = \pounds0.384 billion

0.384 \text{ billion} \times 1,000,000,000 = \pounds384,000,000

Question 9

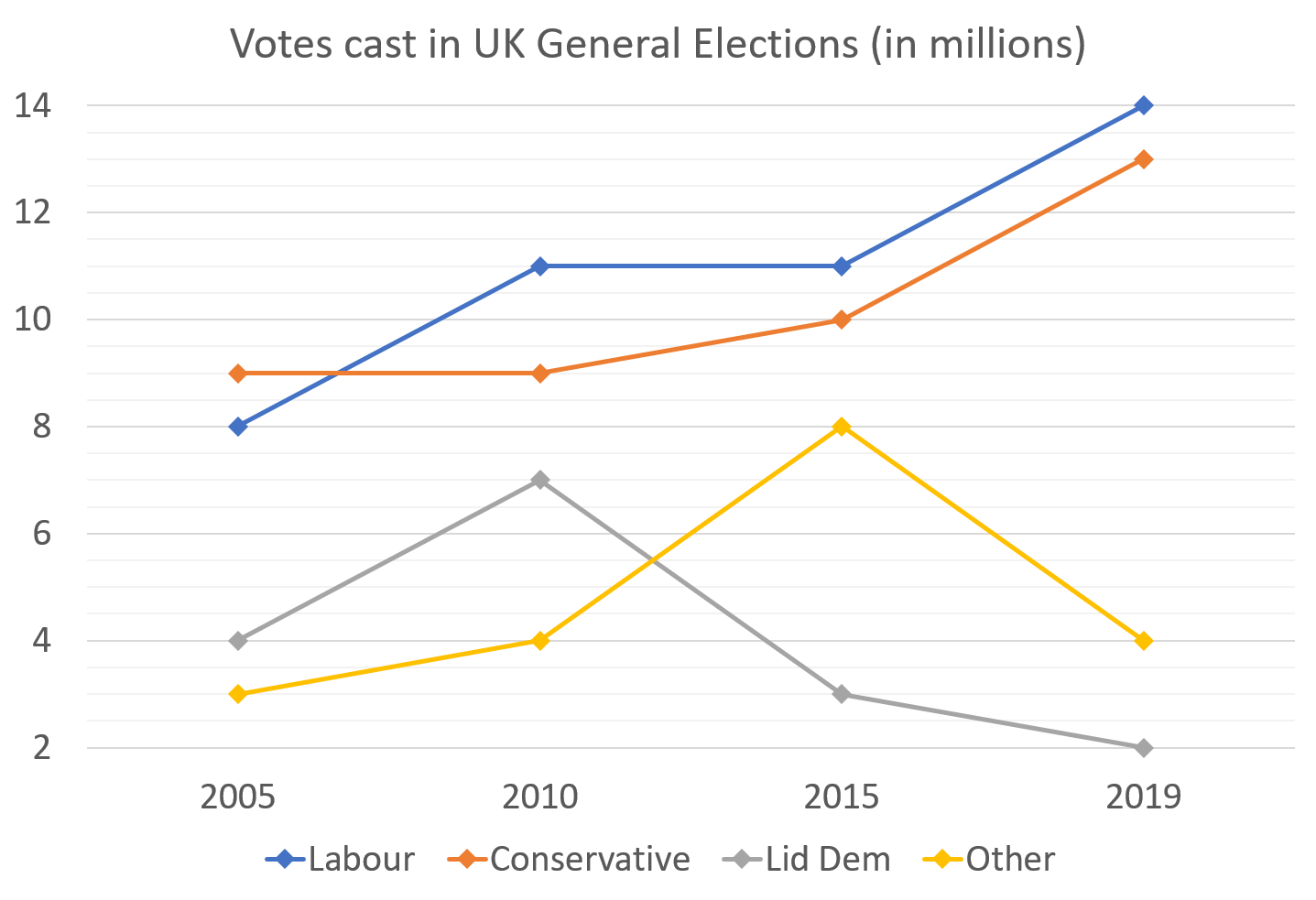
What was the difference in percentages of voter turnout over the period, assuming a voting population of 60m in 2005, that increased by 22% to 2019?

A: 2.16%

B: 3.32%

C: 4.62%

D: 5.08%

Written Solutions

If, in 2005, there was a population of 60 million which increased by 22% in 2019, we can calculate the population in 2019 as follows:

60 million \times 1.22 = 73.2 million

The number of people who voted in 2005 was 9 + 8 + 4 + 3 = 24 million.

The percentage of people who voted in 2005 was:

24 million \div 60 million \times 100 = 40\%

The number of people who voted in 2009 was 14 + 13 + 4 + 2 = 33 million.

The percentage of people who voted in 2009 was:

33 \text{ million} \div 73.2 \text{ million} = 45.08\% .

Therefore the difference in percentages is simply 45.08\% - 40\% = 5.08\%

Question 10

People under 50 years of age and over 50 vote in the ratio 7:4. How many over 50 voters were there in 2019?

A: 12 million

B: 15 million

C: 18 million

D: 21 million

Written Solutions

The number of people who voted in 2009 was 14 + 13 + 4 + 2 = 33 million.

Over 50 voters comprise \frac{4}{11} of the voting population (we are deadline with elevenths because 7 + 4 = 11).

Therefore we can calculate the number of over 50 voters as follows:

33 million \times \frac{4}{11} = 12 million over 50s

Question 11

36% of the vote is required to form a government. In how many of the years was this passed by at least one party?

A: 1

B: 2

C: 3

D: 4

Written Solutions

For this question, we simply need to look at the party that received the most votes are work out whether or not this is greater than or equal to 36\%.

In 2005, the Conservative party received 9 million votes. In total, 9 + 8 + 4 + 3 = 24 million votes were cast.

Therefore, the Conservative party received 9 \div 24 \times 100 = 37.5\% of the vote.

In 2006, the Labour party received 11 million votes. In total, 11 + 9 + 7 + 4 = 31 million votes were cast.

Therefore, the Labour party received 11 \div 31 \times 100 = 35.48\% of the vote.

In 2015, the Labour party received 11 million votes. In total, 11 + 10 + 7 + 4 = 32 million votes were cast.

Therefore, the Labour party received 11 \div 31 \times 100 = 34.375\% of the vote.

In 2019, the Labour party received 14 million votes. In total, 14 + 13 + 4 + 2 = 33 million votes were cast.

Therefore, the Labour party received 14 \div 33 \times 100 = 42.42\% of the vote.

36\% of the overall vote was gained by the winning party in 2005 and 2019, so 2 is the answer.

Question 12

The “Other” category comprises three other parties, A, B and C.  A and B receive votes in the ratio 1 : 2, and B and C receive votes in the ratio of 4 : 7.  To the nearest million, how many votes did party C receive in total in the four elections?

A: 6 million

B: 8 million

C: 10 million

D: 11 million

Written Solutions

Over the 4 elections, the ‘Other’ party received a total of 3 + 4 + 8 + 4 = 19 million votes.

The issue we have with the ratio is that the B share is not the same in both ratios. In the ratio with A, B’s share is 2, whereas in the ratio with C, the B share is 4. We will need to adjust one of the ratios. If A and B receive votes in the ratio of 1 : 2, this is the equivalent of receiving votes in the ratio of 2 : 4. Now we have the same value for the B share in both ratios.

Therefore, the ratio of A : B : C is 2 : 4 : 7. This means that party C received \frac{7}{13} of all the votes (we are dealing with thirteenths because 2 + 4 + 7 = 13).

The number of votes that party C received can be calculated as follows:

19 \text{ million} \times \frac{7}{13} = 10.23 million or 10 million to the nearest million.

Question 13

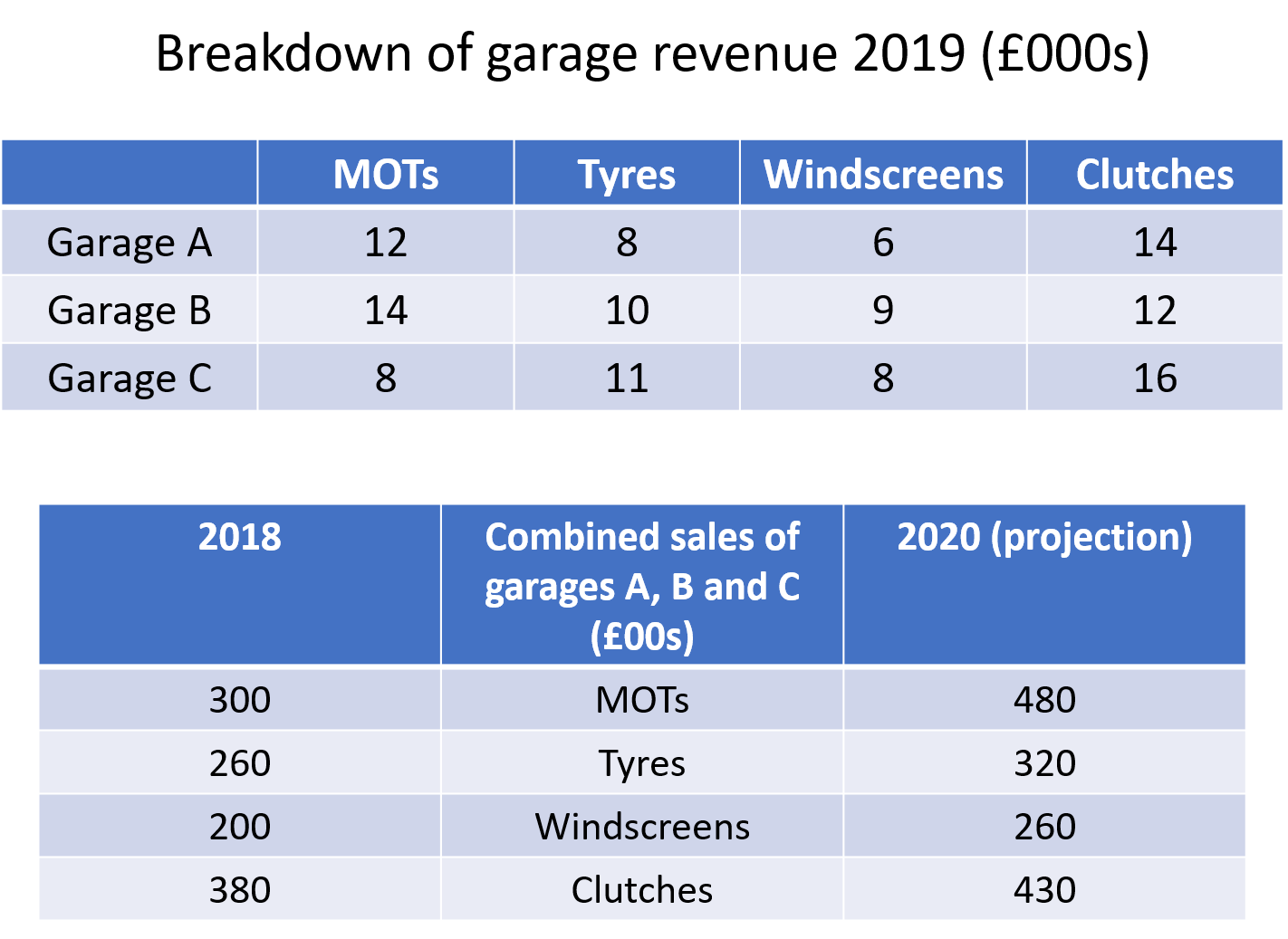
What percentage of the overall sales of the 3 garages combined in 2019 was made from MOT revenue?  Give your answer to one decimal place.

A: 14.6%

B: 19.7%

C: 26.6%

D: 27.9%

Written Solutions

First of all, we need to work out how much money was generated overall by the 3 garages:

12 + 14 + 8 + 8 + 10 + 11 + 6 + 9 + 8 + 14 + 12 + 16 = 128 (thousand)

The total revenue generated from MOTs was:

12 + 14 + 8 = 34 (thousand)

As a percentage, the MOT sales accounted for 34 \div 128 \times 100 = 26.6\%

Question 14

As a percentage, how much more revenue is expected to be generated in 2020 from windscreens than in 2019?  Give your answer to the nearest whole number.

A: 7%

B: 13%

C: 16%

D: 24%

Written Solutions

In 2019, the revenue generated from windscreens was 6 + 9 + 8 = 23 (thousand). The projection for 2020 is 260 (hundred). This question is tricky since the top table is in thousands, whereas the bottom table is in hundreds, so we need to be careful with these figures:

23 \text{ thousand} = 23,000 260 \text{ hundred} = 26,000

The percentage increase in sales is \dfrac{26,000 - 23,000}{23,000} \times 100 = 13.04\% (or 13\% to the nearest whole number.

Question 15

Garage C generated the same percentage of sales in 2019 as in 2018.  How much did garage C make to the nearest pound in 2018?

A: £29,968

B: £35,687

C: £38,297

D: £40,683

Written Solutions

First of all, we need to work out how much money was generated overall by the 3 garages in 2019:

12 + 14 + 8 + 8 + 10 + 11 + 6 + 9 + 8 + 14 + 12 + 16 = \pounds128,000

In 2019, Garage C generated 8 + 11 + 8 + 16 = \pounds43,000

As a percentage, this is \pounds43,000 \div \pounds128,000 \times 100 = 33.59375\%

In 2018, the combined sales of the 3 garages was 300 + 260 + 200 + 380 = \pounds114,000

If Garage C generated 33.59375\% of overall revenue, then Garage C generated \pounds114,000 \times 0.3359375 = \pounds38,296.88 or \pounds38,297 to the nearest pound.

Even if you rounded the 33.59375\% earlier in the question, you would probably get an answer that was pretty close to answer A, and nowhere near answers B, C and D.

Question 16

Revenue in 2020 increase by 3% from 2019.  By how much have the 3 garages missed the overall target for 2020?

A: £9,065

B: £12,784

C: £17,160

D: £21,865

Written Solutions

First of all, we need to work out how much money was generated overall by the 3 garages in 2019:

12 + 14 + 8 + 8 + 10 + 11 + 6 + 9 + 8 + 14 + 12 + 16 = \pounds128,000

If the revenue increases by 3\%, then the 2020 revenue can be calculated as follows:

\pounds128,000 \times 1.03 = \pounds131,840

The 2020 projection was 480 + 320 + 260 + 430 = \pounds149,000

Therefore the garages missed their projection by \pounds149,000 - \pounds131,840 = \pounds17,160

Question 17

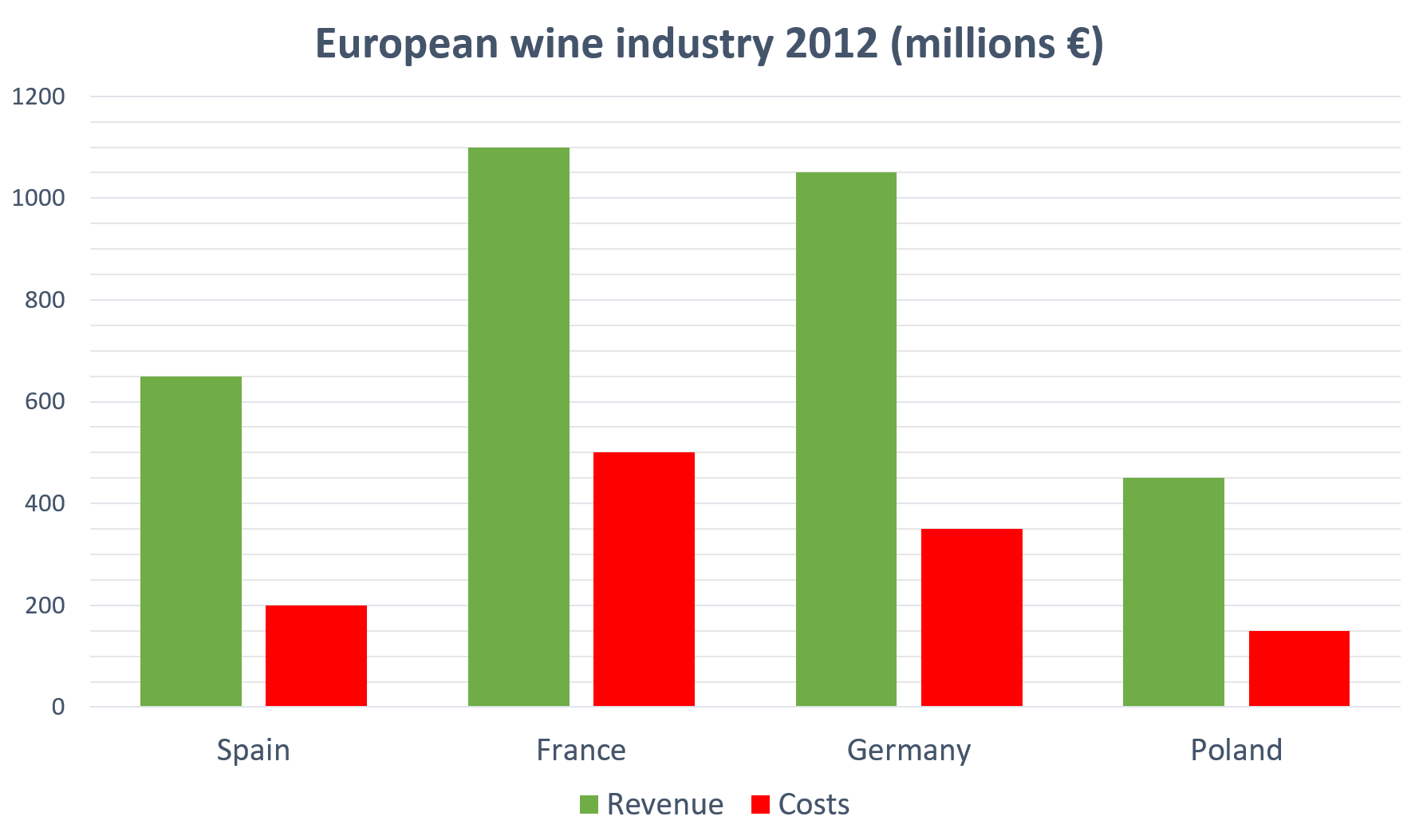
What was the percentage decrease in profit for Spain from 2012 to 2013 if costs increased by 15% but revenue stayed the same?

A: 6.6%

B: 7.75%

C: 12.3%

D: 12.5%

Written Solutions

The profit for Spain was €650 \text{ million} - €200 \text { million} = €450 \text{ million}.

If costs increased by 15\% from €200 million, then the total costs for 2013 can be calculated as follows:

€200 \times 1.15 = €230 million

If in 2013, the costs were €230 million and the revenue remained the same, then the overall profit in 2013 was €650 \text{ million} - €230 \text{ million} = €420 million

If profit decreased from €450 million to €420 million, the percentage decrease can be calculated as follows:

\dfrac {€450 - €420}{€450} \times 100 = 6.6\%

Question 18

The UK has a revenue of £687 million in 2012 and has costs of €65 for every £1,000 of revenue. What is the overall profit for the UK in euros to the nearest million? (€1 is the equivalent of £0.88.)

A: €465 million

B: €524 million

C: €736 million

D: €812 million

Written Solutions

If the UK has costs of €65 for every \pounds1,000 of revenue, we need to work out how many thousands of revenue it generates.

If the UK generates \pounds687,000,000, this is the equivalent of 687,000 thousands of pounds, so the costs incurred would be 687,000 \times €65 = €44,655,000.

If the UK has a revenue of \pounds687 million, this is the equivalent of \pounds687,000,000 \div \pounds0.88 = €780,681,820 .

The overall profit is €780,681,820 - €44,655,000 = €736,026,821 or €736 million to the nearest million.

Question 19

What is the approximate difference in profit of Spain and Poland in 2014 if Spain increases its profit by 3% each year and Poland increases its profit by 12% each year?

A: €46 million

B: €101 million

C: €376 million

D: €477 million

Written Solutions

Spain’s profit in 2012 is €650 - €200 = €450 million.

Poland’s profit in 2012 is €450 -€150 = €300 million.

If Spain increases its profit by 3\% over the following two years, then in 2014 the profit it generates can be calculated as follows:

€450 \text{ million} \times1.03 \times 1.03 = €477.405 million

If Poland increases its profit by 12\% over the following two years, then in 2014 the profit it generates can be calculated as follows:

€300 \text{ million} \times 1.12 \times 1.12 = €376.32 million

Therefore the difference between the profit of the two countries in 2014 is €477.405 - €376.32 = €101.085 million or €101 million euros to the nearest million.

Question 20

Which country’s profit is the highest as a proportion of its revenue in 2012?

A: Spain

B: France

C: Germany

D: Poland

Written Solutions

Spain’s revenue is 650 million. Spain’s profit is €350 - €200 = €450 million.

As a proportion of revenue, Spain’s profit is €450 \div €650 \times 100 = 69.23\%.

France’s revenue is 1100 million. France’s profit is €1100 - €500 = €600 million.

As a proportion of revenue, France’s profit is €600 \div €1100 \times 100 = 54.54\%.

Germany’s revenue is 1050 million. Germany’s profit is €1050 - €350 = €700 million.

As a proportion of revenue, Germany’s profit is €700 \div €1050 \times 100 = 66.6\%.

Poland’s revenue is 450 million. Poland’s profit is €450 - €150 = €300 million.

As a proportion of revenue, Poland’s profit is €300 \div €450 \times 100 = 66.6\%.

Therefore, Spain has the biggest profit as a proportion of its revenue.