Question 1

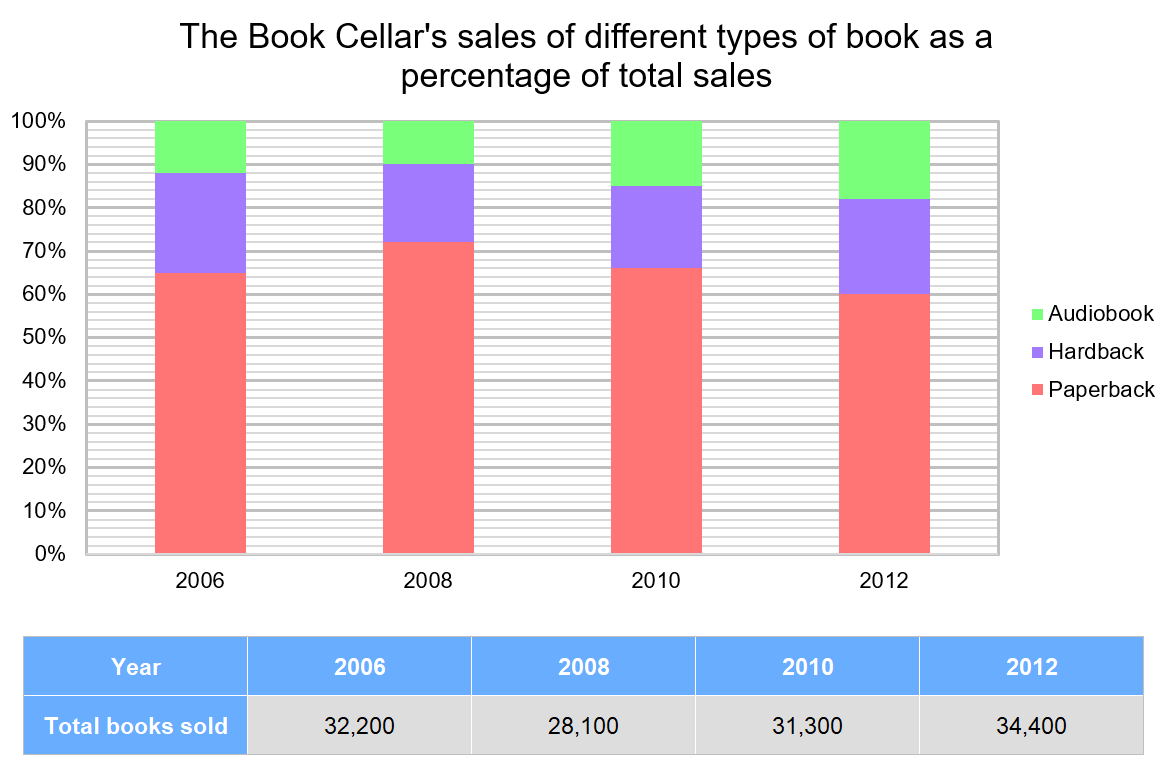
At the end of 2008, The Book Cellar introduced a new online feature to increase the accessibility of audiobooks. The aim was to increase the sales of audiobooks by 40% every 2 years after 2008. In which years did they meet or surpass their target?

A: 2010 only

B: 2012 only

C: Both 2010 and 2012

D: Neither 2010 nor 2012

Written Solutions

Step 1: Find the number of audiobooks sold in 2008, 2010, and 2012.

2008: 100 - 90 = 10\% \text{ so, } 0.10 \times 28,100 = 2,810 \text{ audiobooks sold}

2010: 100 - 85 = 15\% \text{ so, } 0.15 \times 31,300 = 4,695 \text{ audiobooks sold}

2012: 100 - 82 = 18\% \text{ so, } 0.18 \times 34,400 = 6,192 \text{ audiobooks sold}

Step 2: Calculate what a 40% increase would look like in 2010 and 2012.

A 40% increase corresponds to a multiplier of 1.40.

2010: 2,810 \times 1.40 = 3,934 \text{ audiobooks sold}

2012: 4,695 \times 1.40 = 6,573 \text{ audiobooks sold}

Step 3: Identify the years they met/surpassed their target.

2010: 4,695 \geq 3,934 \checkmark

2012: 6,192 < 6,573 \times

Thus, they only met their target in 2010.

Question 2

The average profit made by The Book Cellar on a paperback book is £2.40. This increases by 15% for an audiobook and then by a further £2.06 for a hardback. What is the profit made from sales of paperback books in 2006 as a proportion of that year’s total profits?

A: 52.0%

B: 48.7%

C: 55.1%

D: 53.6%

Written Solutions

Step 1: Calculate how many books of each type were sold in 2006.

100 - 88 = 12\% \text{ so, } 0.12 \times 32,200 = 3,864 \text{ audiobooks sold}

88 - 65 = 23\% \text{ so, } 0.23 \times 32,200 = 7,406 \text{ hardbacks sold}

0.65 \times 32,200 = 20,930 \text{ paperbacks sold}

 

Step 2: Work out the profit made on audiobooks and hardbacks.

A 15% increase corresponds to a multiplier of 1.15.

\text{Profit on audiobook } = 2.40 \times 1.15 = \pounds 2.76

\text{Profit on hardback } = 2.76 + 2.06 = \pounds 4.82

Step 3: Calculate the total profit made on each type of book.

\text{Audiobook profit } = 3,864 \times 2.76 = \pounds 10,664.64

\text{Hardback profit } = 7,406 \times 4.82 = \pounds 35,696.92

\text{Paperback profit } = 20,930 \times 2.40 = \pounds 50,232

Step 4: Calculate the proportion of the total profit that is due to paperback sales.

\dfrac{50,232}{10,664.64 + 35,696.92 + 50,232} \times 100 = 52.0\%

Question 3

Sales of hardback books are split between fiction and non-fiction according to the ratio 5:4. In 2014, 3,608 hardback non-fiction books were sold. Given that the proportions of sales for each type of book remained the same as in 2012, how many more books were sold in 2014 than in 2012?

A: 2,500

B: 2,600

C: 2,700

D: 2,800

Written Solutions

Step 1: Calculate the number of hardback books sold in 2014.

As the ratio is 5:4, the 3,608 hardback non-fiction books constitute 4 parts of the whole. Therefore,

\text{1 part } = 3,608 \div 4 = 902.

There are 5 + 4 = 9 parts in total, so we get

\text{Hardbacks sold in 2014 } = 902 \times 9 = 8,118

Step 2: Work out how many books were sold in 2014.

Proportions are the same as in 2012, and in 2012 82\% - 60\% = 22\% of all books were hardbacks. The total number of books sold in 2014 multiplied by 0.22 must equal 8,118, so to find the total we must divide by 0.22.

\text{Total book sales in 2014 } = 8,118 \div 0.22 = 36,900

Step 3: Find the difference between the 2014 sales and 2012 sales.

36,900 - 34,400 = 2,500

Question 4

Paperback books sold for an average of £7.85, £7.90 and £8.14 in 2006, 2008, and 2010 respectively. What is the ratio in revenue from sales of paperback books in 2006 compared to 2008 and 2010?

A: 1.01 : 1 : 1.03

B: 1.02 : 1 : 1.06

C: 1.04 : 1 : 1.09

D: 1.03 : 1 : 1.05

Written Solutions

Step 1: Calculate how many paperbacks were sold in 2006, 2008, and 2010.

\text{2006 paperback sales } = 0.65 \times 32,200 = 20,930

\text{2008 paperback sales } = 0.72 \times 28,100 = 20,232

\text{2010 paperback sales } = 0.66 \times 31,300 = 20,658

Step 2: Work out the revenue from paperbacks in each year.

\text{2006 paperback revenue } = 20,930 \times 7.85 = \pounds 164,300.50

\text{2008 paperback revenue } = 20,232 \times 7.90 = \pounds 159,832.80

\text{2010 paperback revenue } = 20,658 \times 8.14 = \pounds 168,156.12

Step 3: Form the ratio and simplify by dividing through by the smallest element.

\begin{aligned}\text{2006 : 2008 : 2010 } &= 164,300.50 : 159,832.80 : 168,156.12 \\ &= \dfrac{164,300.50}{159,832.80} : \dfrac{159,832.80}{159,832.80} : \dfrac{168,156.12}{159,832.80} \\ &= 1.03 : 1 : 1.05 \end{aligned}

Question 5

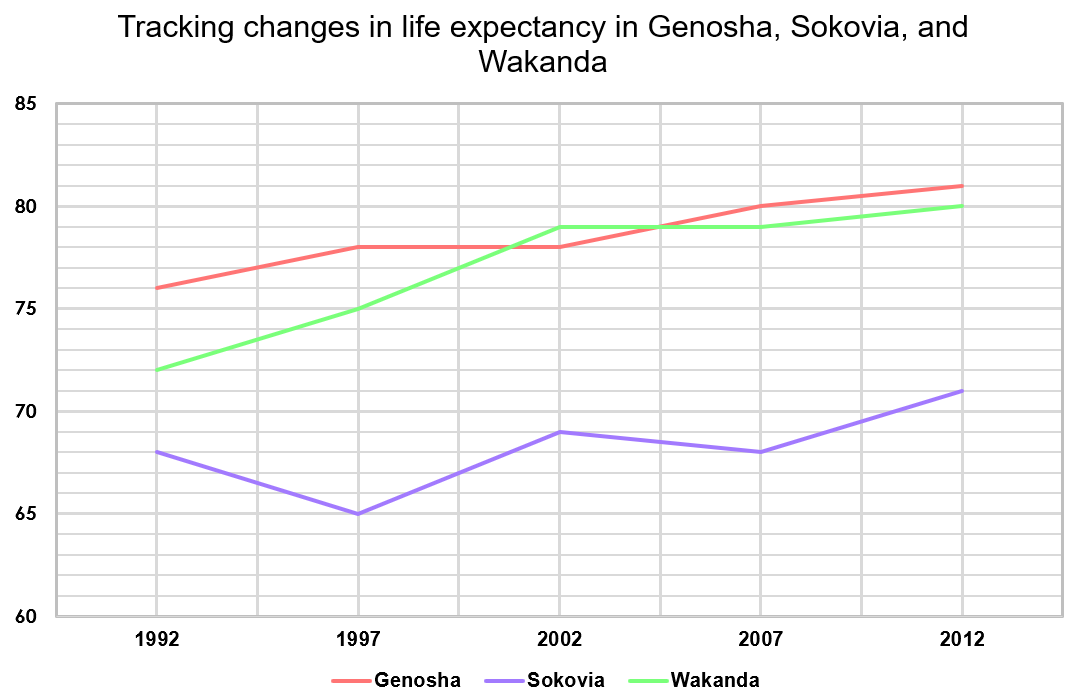
The population in Wakanda in 1997 was 86,058,000. Assuming a 6% population growth every 5 years, what is the ratio of the entire population’s life expectancies added together in 1997 compared to 2007 and 2012.

A: 1 : 1.18 : 1.22

B: 1 : 1.18 : 1.27

C: 1 : 1.19 : 1.25

D: 1 : 1.15 : 1.25

Written Solutions

Step 1: Calculate the population in Wakanda in 2007 and 2012.

A 6% population growth corresponds to a multiplier of 1.06. 2007 is 10 years on and 2012 is 15 years on, so we will have to apply the multiplier twice for 2007 and then once more for 2012.

\text{2007 population } = 86,058,000 \times 1.06^2 = 96,694,769

\text{2012 population } = 96,694,769 \times 1.06 = 102,496,455

Step 2: Calculate the sum of the whole population’s life expectancies in each year.

1997: 86,058,000 \times 75 = 6,454,350,000 \text{ years}

2007: 96,694,769 \times 79 = 7,638,886,751 \text{ years}

2012: 102,496,455 \times 80 = 8,199,716,400 \text{ years}

Step 3: Form the ratio and simplify by dividing through by the smallest element.

\begin{aligned} \text{1997 : 2007 : 2012 } &= 6,454,350,000 : 7,638,886,751 : 8,199,716,400 \\ &= \dfrac{6,454,350,000}{6,454,350,000} : \dfrac{7,638,886,751}{6,454,350,000} : \dfrac{8,199,716,400}{6,454,350,000} \\ &= 1 : 1.18 : 1.27 \end{aligned}

Question 6

After 1997, Sokovia decided to spend $60m per year to increase life expectancy. They would go on to up the spending by $10m after the first 5 years and then by another $10m every 2 years after that. Given these figures, what was the average cost per year of increased life expectancy in Sokovia from 1997 to 2012 inclusive?

A: $193m

B: $213m

C: $207m

D: $200m

Written Solutions

Step 1: Determine how much was spent on trying to increase life expectancy from 1997 to 2002.

The first 5 years saw $60m being spent per year, thus:

\text{1998-2002 spend } = 60\text{m } \times 5 = \$ 300\text{m}

Step 2: Determine how much was spent from 2003 to 2012, and therefore the total spend.

At the start of this 10-year period, spending was $70m. This lasted for 2 years, and then increased to $80m, which also lasted for 2 years, and so on. Therefore these 10 years can be broken down as such: 2 years of spending $70m, 2 years of $80m, 2 years of $90m, 2 years of $100m, and 2 years of $110m. So, we get:

\begin{aligned}\text{2003-2012 spend } &= ((2 \times 70) + (2 \times 80) + (2 \times 90) \\ & + (2 \times 100) + (2 \times 110)) \text{ million } \\ &= \$ 900 \text{m}\end{aligned}

\text{Total spend } = 900\text{m } + 300\text{m } = \$ 1,200\text{m }

Step 3: Find the average cost per year of increased life expectancy.

\text{Life expectancy increase } = 71 - 65 = 6 \text{ years}

\text{Cost per year of increase } = \dfrac{1,200\text{m}}{6} = \$ 200\text{m}

Question 7

If all 3 countries’ life expectancies continued to grow at the same percentage rate after 2012 as they did from 2007 to 2012, what would the difference have been between the country with the highest life expectancy and the one with the lowest in 2017?

A: 7.4 years

B: 7.6 years

C: 7.8 years

D: 8.0 years

Written Solutions

Step 1: Work out the percentage increase in each country from 2007 to 2012.

Sokovia: \dfrac{71 - 68}{68} \times 100 = 4.41\%

Wakanda: \dfrac{80 - 79}{79} \times 100 = 1.27\%

Genosha: \dfrac{81 - 80}{80} \times 100 = 1.25\%

Step 2: Calculate the life expectancies for all 3 countries in 2017.

A 4.41% increase corresponds to a multiplier of 1.0441; a 1.27% increase corresponds to a multiplier of 1.0127; a multiplier of 1.25% corresponds to a multiplier of 1.0125. Therefore:

\text{2017 Sokovian life expectancy } = 71 \times 1.0441 = 74.1311 \text{ years}

\text{2017 Wakandan life expectancy } = 80 \times 1.0127 = 81.016 \text{ years}

\text{2017 Genoshan life expectancy } = 81 \times 1.0125 = 82.0125 \text{ years}

Step 3: Subtract the smallest value from the largest value.

82.0125 - 74.1311 \simeq 7.8 \text{ years}

Question 8

The life expectancy in Genosha in 1992 constitutes a 3% increase on the life expectancy for 1987. If the ratio of life expectancies between the 2 countries in 1987 is the same as it was for 1997, what was the percentage increase in life expectancy in Wakanda from 1987 to 1992?

A: 1.4%

B: 1.5%

C: 1.6%

D: 1.8%

Written Solutions

Step 1: Work out the life expectancy in Genosha in 1987.

A 3% increase corresponds to a multiplier of 1.03. As the 1992 life expectancy of 76 is a result of this 3% increase, we must divide by 1.03 in order to obtain the 1987 value.

\text{1987 Genoshan life expectancy } = 76 \div 1.03 = 73.79 \text{ years}

Step 2: Work out the life expectancy in Wakanda in 1987.

The ratio of life expectancy in Genosha to Wakanda was the same as it was in 1997 i.e. it was 78:75 = 26:25. Genosha’s 73.79-year life expectancy constitutes 26 parts of this ratio, so we get:

\text{1 part } = 73.79 \div 26 = 2.838 \text{ years}

Wakanda makes up 25 parts of the ratio, so:

\text{1987 Wakandan life expectancy } = 2.838 \times 25 = 70.95 \text{ years}.

Step 3: Determine the percentage increase in Wakandan life expectancy.

\dfrac{72 - 70.95}{70.95} \times 100 = 1.5\%

Question 9

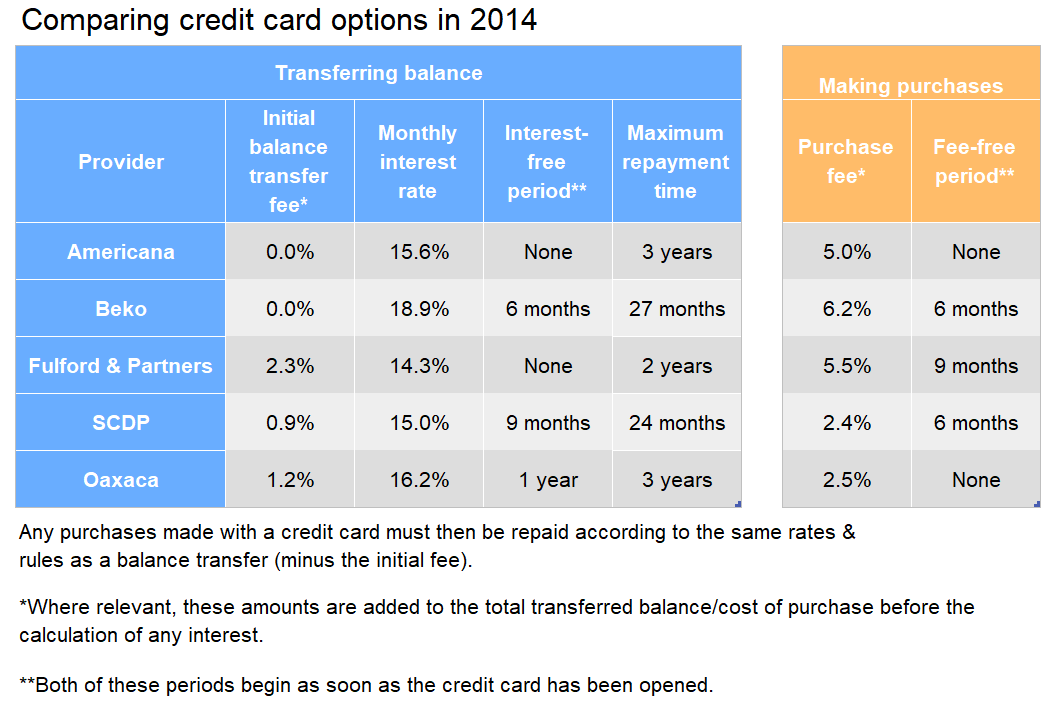
If someone wishes to transfer a balance of £3,500 to a new credit card and repay that debt over the course of 28 months, what is the ratio of the extra costs (i.e., those on top of the £3,500 repayment) for their cheapest option compared to the extra payments for their most expensive option?

A: 1 : 1.62

B: 1 : 1.48

C: 1 : 1.32

D: 1 : 1.21

Written Solutions

Step 1: For a 28-month repayment plan, they have 2 options: Americana or Oaxaca. Work out the extra costs for an Americana repayment.

With an Americana credit card, there is no initial balance transfer fee, but also no interest-free period. The result of this is that the total extra cost is 15.6% of all monthly payments, which is equivalent to 15.6% of the total balance transfer – £3,500.

15.6\% = 0.156, so:

\text{Americana extra costs } = 0.156 \times 3,500 = \pounds 546

Step 2: Work out the extra costs for an Oaxaca repayment.

A 1.2% increase corresponds to a multiplier of 1.012.

\text{Balance transfer + fee } = 3,500 \times 1.012 = \pounds 3,542

A 16.2% increase corresponds to a multiplier of 1.162.

\text{Base monthly cost } = 3,542 \div 28 = \pounds 126.50

\text{Monthly cost with interest } = 126.50 \times 1.162 = \pounds 146.99

The first 12 months are interest-free, so the latter 28 - 12 = 16 months have interest added on. Therefore:

\text{Total payment } = (12 \times 126.50) + (16 \times 146.99) = \pounds 3,869.84

\text{Oaxaca extra costs } = 3,869.84 - 3,500 = \pounds 369.84

Step 3: Form the ratio and simplify by dividing through by the smallest element.

\begin{aligned}\text{Lowest extra costs : highest extra costs } &= 369.84 : 546 \\ &= \dfrac{369.84}{369.84} : \dfrac{546}{369.84} \\ &= 1 : 1.48\end{aligned}

Question 10

A woman opens an SCDP credit account with no balance transfer. 5 months after opening this account, she uses that credit card to pay for a holiday worth £2,850. Work out the percentage saving she makes on her total repayment if she repays her holiday payment in 10 months rather than 20.

A: 2.68%

B: 2.74%

C: 3.02%

D: 3.45%

Written Solutions

Step 1: Calculate her total repayment if she repays the holiday in 10 months.

Making the payment after 5 months means she avoids the purchase fee, but there are only 4 remaining interest-free months. For the interest: a 15% increase corresponds to a multiplier of 1.15.

\text{Base monthly cost } = 2,850 \div 10 = \pounds 285

\text{Monthly cost with interest } = 285 \times 1.15 = \pounds 327.75

She pays no interest for the first 4 months, so the latter 10 - 4 = 6 will have interest added on. Therefore:

\text{10-month repayment total } = (4 \times 285) + (6 \times 327.75) = \pounds 3,106.50

Step 2: Calculate her total repayment if she repays the holiday in 20 months.

As before, there’s no purchase fee and there are only 4 remaining interest-free months. For this: a 15% increase corresponds to a multiplier of 1.15.

\text{Base monthly cost } = 2,850 \div 20 = \pounds 142.50

\text{Monthly cost with interest } = 142.50 \times 1.15 = \pounds 163.88

She pays no interest for the first 4 months, so the latter 20 - 4 = 16 months will have interest added on. Therefore:

\text{20-month repayment total } = (4 \times 142.50) + (16 \times 163.88) = \pounds 3,192.08

Step 3: Work out the percentage saving.

\dfrac{3,192.08 - 3,106.50}{3,192.08} \times 100 = 2.68 \%

Question 11

What is the difference between the average daily payment required for a Fulford & Partners credit card and a Beko credit card if you transfer a balance of £5,000 and repay the full amount back over the course of 18 months? You may assume 30 days in a month.

A: £0.40

B: £0.55

C: £0.65

D: £0.80

Written Solutions

Step 1: Work out the average daily payment for a Fulford & Partners card.

Firstly, the balance transfer fee. A 2.3% increase corresponds to a multiplier of 1.023.

\text{Balance transfer with fee } = 5,000 \times 1.023 = \pounds 5,115

There are no interest-free months, so the 14.3% interest rate is applied to every monthly payment. In other words, we can apply it to the whole value of the balance transfer. A 14.3% increase corresponds to a multiplier of 1.143.

\text{Fulford \& Partners total } = 5,115 \times 1.143 = \pounds 5,846.45

This will be repaid over the course of 18 \times 30 = 540 days, so:

\text{Average daily payment } = \dfrac{5,846.45}{540} = \pounds 10.83

Step 2: Work out the average daily payment for a Beko credit card.

There is no balance transfer fee.

There are 6 months of interest-free payments, so there will be 18 - 6 = 12 months of payments with interest added. An increase of 18.9% corresponds to a multiplier of 1.189.

\text{Base monthly cost } = 5,000 \div 18 = \pounds 277.78

\text{Monthly cost with interest } = 277.78 \times 1.189 = \pounds 330.28

6 months of interest-free payments followed by 12 payments with interest gives:

\text{Beko total } = (6 \times 277.78) + (12 \times 330.28) = \pounds 5,630.04

\text{Average daily payment } = \dfrac{5,630.04}{540} = \pounds 10.43

Step 3: Find the difference.

\text{Difference } = 10.83 - 10.43 = \pounds 0.40

Question 12

A man opens a credit account with Oaxaca and after 1 month makes a purchase of £6,400. In the 13th month of his repayment, he pays £238.21. Assuming the same repayment time, how much more money would he have to repay in the 13th month if he had made the purchase with an Americana account?

A: £3.45

B: £3.78

C: £4.55

D: £4.95

Written Solutions

Step 1: Find the length of his Oaxaca repayment.

The purchase fee of 2.5% corresponds to a multiplier of 1.025.

\text{Purchase + fee } = 6,400 \times 1.025 = \pounds 6,560

The cost of his 13th repayment will have 16.2% interest added to it, i.e. it will have been multiplied by 1.162 (the corresponding multiplier). In order the find the cost without interest, we must divide by 1.162.

\text{Base monthly cost } = 238.21 \div 1.162 = \pounds 205.

\text{Therefore, length of repayment } = \dfrac{6,560}{205} = 32 \text{ months}.

Step 2: Calculate the cost in the 13th month with an Americana credit card.

The 5% purchase fee corresponds to a multiplier of 1.05.

\text{Purchase + fee } = 6,400 \times 1.05 = \pounds 6,720

There will be interest added in the payment of the 13^th month (there’s no interest-free period, in fact). A 15.6% increase corresponds to a multiplier of 1.156.

\text{Base monthly cost } = 6,720 \div 32 = \pounds 210

\text{Cost in 13th month } = 210 \times 1.156 = \pounds 242.76

Step 3: Find the difference.

\text{Difference in 13th month } = 242.76 - 238.21 = \pounds 4.55

Question 13

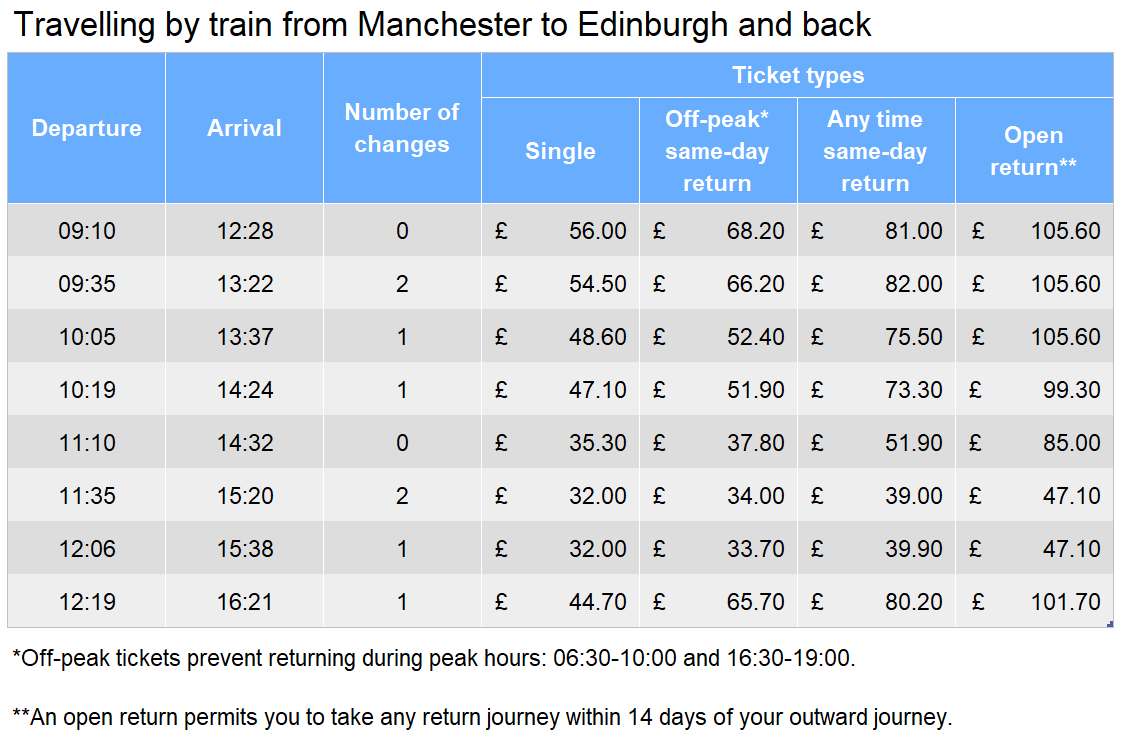
Adam and Barry both leave for Edinburgh before 10:30am. They both spend exactly 5 hours in the city, at which point they leave the city by train. Adam buys the cheapest return ticket possible, whilst Barry chooses the shortest outward journey, and then buys the cheapest possible return ticket. Given these conditions, what is the cost of Adam’s ticket as a proportion of Barry’s?

A: 82.3%

B: 54.0%

C: 64.1%

D: 60.1%

Written Solutions

Step 1: Determine the cost of Adams’s ticket.

The cheapest journey option is the 10:19 departure. He would then arrive at 14:24.

14:24 + 5 \text{ hours } = 19:24, which is outside of peak times, meaning Adam is able to buy an off-peak ticket.

\text{Cost of Person A’s ticket } = \pounds 51.90

Step 2: Determine the cost of Barry’s ticket.

Firstly, we must identify the shortest journey which leaves before 10:30am.

09:10 departure: 12:28 - 09:10 = 03:18

09:35 departure: 13:22 - 09:35 = 03:47

10:05 departure: 13:37 - 10:05 = 03:32

10:19 departure: 14:24 - 10:19 = 04:05

So, the 09:10 departure is the shortest. He will arrive in Edinburgh at 12:28.

12:28 + 5 \text{ hours } = 17:28, which is during peak hours, meaning he will have to buy an any-time same-day return.

\text{Cost of Barry’s ticket } = \pounds 81.00

Step 3: Calculate the proportion in question.

\dfrac{51.90}{81.00} \times 100 = 64.1\%

Question 14

Journeys with 1 change require a wait of 12 minutes at the connecting station, whilst journeys with 2 changes require a total of 17. Assuming all journeys are 347km, and considering only the time spent on the train, what is the ratio of the average speed travelled on the 11:10 departure journey compared to the 11:35 and 12:06 departures?

A: 1.05 : 1 : 1.06

B: 1.02 : 1 : 1.06

C: 1.03 : 1 : 1.07

D: 1.03 : 1 : 1.04

Written Solutions

Step 1: Work out the time spent on the train for the 3 journeys.

Firstly, find their total lengths:

11:10 departure: 14:32 - 11:10 = 03:22\text{ or }(3 \times 60)+22 = 202 \text{ minutes}

11:35 departure: 15:20 - 11:35 = 03:45\text{ or }(3 \times 60)+45 = 225 \text{ minutes}

12:06 departure: 15:38 - 12:06 = 03:32\text{ or }(3 \times 60)+32 = 212 \text{ minutes}

Now, subtracting time spent waiting at connecting stations:

11:10 departure has 0 stops: \text{length } = 202 \text{ minutes}

11:35 departure has 2 stops: \text{length } = 225 - 17 = 208 \text{ minutes}

12:06 departure has 1 stop: \text{length } = 212 - 12 = 200 \text{ minutes}

Step 2: Calculate their average speeds.

NOTE: because a ratio has no units, we don’t have to work out the speed in km per hour. Instead, to save time, here we will do it in km per minute.

11:10 departure: \text{average speed } = \dfrac{347}{202} = 1.718

11:35 departure: \text{average speed } = \dfrac{347}{208} = 1.668

12:06 departure: \text{average speed } = \dfrac{347}{200} = 1.735

Step 3: Form the ratio and simplify by dividing through by the smallest element.

\begin{aligned}\text{11:10 speed : 11:35 speed : 12:06 speed } &= 1.718 : 1.668 : 1.735 \\ &= \dfrac{1.718}{1.668} : \dfrac{1.668}{1.668} : \dfrac{1.735}{1.668} \\ &= 1.03 : 1 : 1.04 \end{aligned}

Question 15

Work out the difference between the highest cost per minute of outward travel and the lowest cost per minute of outward travel when purchasing an open return for a train with fewer than 2 changes.

A: £0.31

B: £0.30

C: £0.29

D: £0.28

Written Solutions

Step 1: Determine the length, in minutes, of each journey with fewer than 2 stops.

09:10 departure: 12:28 - 09:10 = 03:18\text{ or }(3\times60) + 18 = 198\text{ minutes}

10:05 departure: 13:37 - 10:05 = 03:32\text{ or }(3\times60) + 32 = 212\text{ minutes}

10:19 departure: 14:24 - 10:19 = 04:05\text{ or }(4\times60) + 5 = 245\text{ minutes}

11:10 departure: 14:32 - 11:10 = 03:22\text{ or }(3\times60) + 22 = 202 \text{ minutes}

12:06 departure: 15:38 - 12:06 = 03:32\text{ or }(3\times60) + 32 = 212 \text{ minutes}

12:19 departure: 16:21 - 12:19 = 04:02\text{ or }(4\times60) + 2 = 242 \text{ minutes}

Step 2: Find the lowest and highest cost per minute.

The 12:06 departure is by far the cheapest ticket and is of moderate length. Therefore, we can infer that it has the lowest cost per minute at \dfrac{47.10}{212} = \pounds 0.22.

The 09:10 departure is the shortest journey whilst also being the (joint) most expensive. Therefore, it must have the highest cost per minute at \dfrac{105.60}{198} = \pounds 0.53.

Step 3: Work out the difference.

\text{Difference in cost per minute } = \pounds 0.53 - \pounds 0.22 = \pounds 0.31

Question 16

A group of 24 friends are going on a trip to Edinburgh on the 10:05 train. According to the ratio 3:2:1, they are split between leaving that same day at 10pm, staying for one night, and staying for 5 nights. If they all choose the cheapest possible return ticket, and their hotel costs £35 per person per night, what is average cost per person for this trip?

A: £124.92

B: £124.60

C: £121.34

D: £119.83

Written Solutions

Step 1: Work out the cost of all the train tickets.

The ratio of 3:2:1 has 6 parts in total. We can multiply 6 by 4 to get 24, so if we multiply each component of the ratio by 4 we get a 12:8:4 split between the people described in the question.

Those 12 who are leaving at 10pm on the same day can buy off-peak returns for £52.40. The other 12 will have to purchase open returns for £105.60. So, we get:

\text{Cost of tickets } = (12 \times 52.40)+(12 \times 105.60) = \pounds 1,896

Step 2: Work out the cost of the hotel.

With the ratio of 3:2:1 = 12:8:4, we can see firstly that 12 people won’t spend anything. For those 8 staying one night:

\text{Cost } = 8 \times 35 = \pounds 280

For those 4 staying 5 night:

\text{Cost } = 4 \times (5 \times 35) = \pounds 700

\text{Therefore, hotel cost } = 280 + 700 = \pounds 980

Step 3: Calculate the average cost per person.

\text{Total cost } = 1,896 + 980 = \pounds 2,876

\text{Average cost per person } = \dfrac{2,876}{24} = \pounds 119.83

Question 17

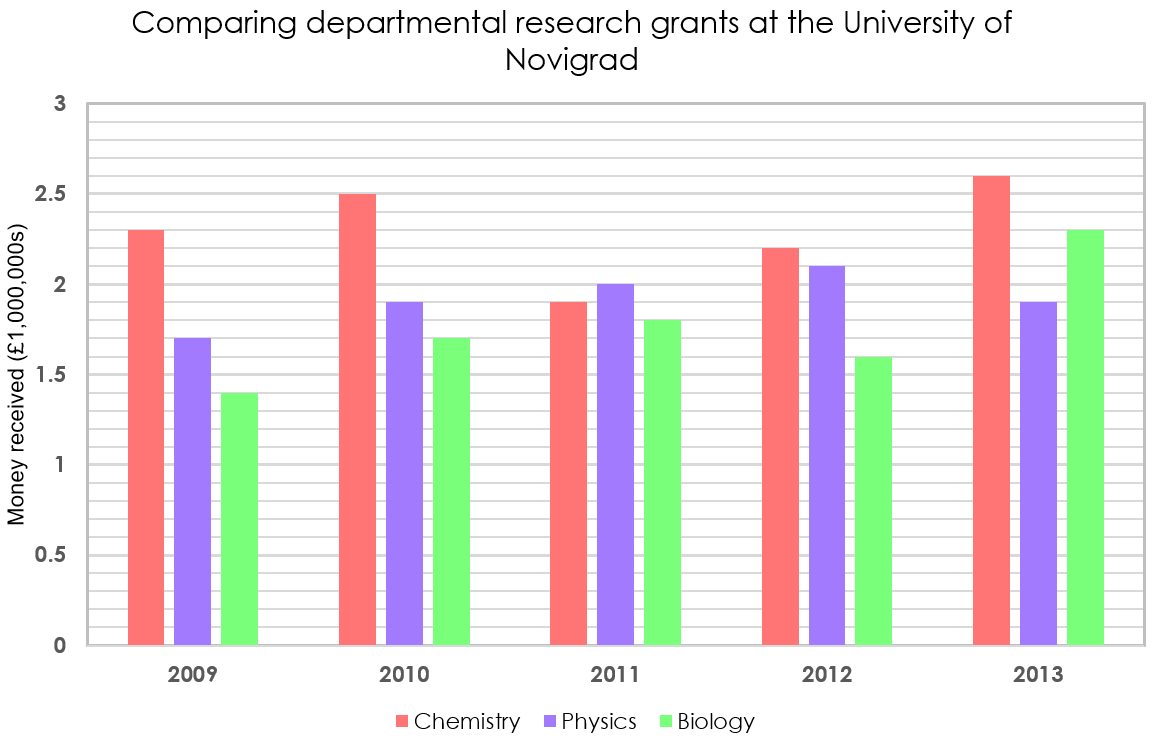
Biochemistry research receives consistent funding each year. After 2010, the researchers in Biochemistry moved from the Chemistry department to the Biology department. Given that the total grants to the Chemistry department are 15% lower in 2011 & 2012 due to this shift, what proportion of the Biology research grants across 2011, 2012, and 2013 are for Biochemistry?

A: 19.0%

B: 22.3%

C: 18.4%

D: 15.3%

Written Solutions

Step 1: Calculate how much grant money is dedicated to Biochemistry research.

\text{Total for Chemistry in 2011 + 2012 } = 1.9 + 2.2 = \pounds 4.1\text{m}

A 15% decrease corresponds to a multiplier of 0.85. If this current value is 15% lower than it otherwise would’ve been, then in order to find the value without this 15% removed we must divide by 0.85.

\text{Total with the 15\% replaced } = 4.1 \div 0.85 = \pounds 4.824\text{m}

\text{Biochemistry grant in 2011 + 2012 } = 4.8235 - 4.1 = \pounds 0.7235\text{m}

Step 2: Calculate the required proportion.

Biochemistry funding is the same every year. So, we get the following.

\text{1 year’s Biochemistry grant } = 0.7235 \div 2 = \pounds 0.36175\text{m}

\text{3 year’s Biochemistry grant } = 0.36175 \times 3 = \pounds 1.08525\text{m}

\text{2011-2013 total biology grant } = 1.8 + 1.6 + 2.3 = \pounds 5.7\text{m}

So, the proportion of Biology grants that are for Biochemistry (note: since a percentage has no units, we don’t need to turn the values into millions, for ease we work with the shorter decimals):

\dfrac{1.08525}{5.7} \times 100 = 19.0\%

Question 18

In 2009, Physics grants were split between postgrad and postdoc research according to the ratio 5:11. In 2009 there were 18 Physics postgrads, but by investing £80,000 in postgrad research each year, this number was increased by 2 each year for the next 5 years. Work out the difference between the average cost of research per postgraduate student in 2009 and 2012.

A: £3,084

B: £2,959

C: £2,621

D: £2,458

Written Solutions

Step 1: Calculate the amount spent on postgrad research in 2009 and 2012.

In the ratio 5:11, there are 5 + 11 = 16 \text{ parts}, so:

\text{1 part } = 1.7 \div 16 = \pounds 0.10625\text{m}

Postgrad research makes up 5 parts of the ratio so:

\text{2009 postgrad research spend } = 0.10625 \times 5 = \pounds 0.53125\text{m}

By 2012, the spending had been upped by £80,000 (or £0.08m) three times.

\text{2012 postgrad research spend } = 0.53125 + (3 \times 0.08) = \pounds 0.77125\text{m}

Step 2: Work out the average cost per postgrad in 2009 and 2012.

\text{2009 cost per postgrad } = \dfrac{0.53125}{18} = \pounds 0.029514\text{m}

By 2012, the number of postgrads had increase by 2 three times.

\text{Number of postgrads in 2012 } = 18 + (3 \times 2) = 24

\text{2012 cost per postgrad } = \dfrac{0.77125}{24} = \pounds 0.032135\text{m}

Step 3: Find the difference.

\text{2012 - 2009 } = 0.032135 - 0.029514 =\pounds 0.002621\text{m} = \pounds 2,621

Question 19

All 50 Biology researchers must perform some teaching duties. If three quarters of all grant money in 2013 was used to pay them for their research, and they earned £23 per hour of research, what is the ratio of research hours to teaching hours for an average researcher? Assume 40 working hours per week and 48 working weeks a year.

A: 4.13 : 1

B: 4.02 : 1

C: 3.94 : 1

D: 3.57 : 1

Written Solutions

Step 1: Determine how many research hours were conducted by the average biology researcher in 2013.

\text{Total paid to members for research } = \dfrac{3}{4} \times 2.3 = \pounds 1.725\text{m}

\text{Number of hours spent researching } = 1.725\text{m} \div 23 = 75,000

\text{Hours per researcher } = 75,000 \div 50 = 1,500

Step 2: Work out how many teaching hours were conducted by the average researcher.

\text{Total working hours in one year } = 40 \times 48 = 1,920

\text{Hours spent teaching } = 1,920 - 1,500 = 420

Step 3: Form the ratio and simplify by dividing through by the smallest element.

\begin{aligned}\text{Research hours : teaching hours } &= 1,500 : 420 \\ &=\dfrac{1,500}{420} : \dfrac{420}{420} \\ &= 3.57 : 1 \end{aligned}

Question 20

In 2011, the Maths department received 5% less money in grants than the Physics department, but their total then increased by 8% each subsequent year. What is the percentage growth in the total value of grants given to all 4 departments (Physics, Chemistry, Biology, Maths) from 2011 to 2013?

A: 21.0%

B: 20.2%

C: 19.4%

D: 18.6%

Written Solutions

Step 1: Calculate total grant money received in 2011 by all 4 departments.

In 2011, the Physics department received £2m. A 5% decrease corresponds to a multiplier of 0.95.

\text{2011 Maths research grant } = 2 \times 0.95 = \pounds 1.9\text{m}

\text{2011 total grants received } = 1.9 + 1.9 + 2 + 1.8 = \pounds 7.6\text{m}

Step 2: Calculate the total grant money received in 2013 by all 4 departments.

A yearly growth of 8% corresponds to a multiplier of 1.08. Because we are looking for the 2013 value, we must apply this multiplier twice.

\text{2013 Maths research grant } = 1.9 \times 1.08^2 = \pounds 2.21616\text{m}

\text{2013 total grants received } = 2.21616 + 2.6 + 1.9 + 2.3 = \pounds9.01616 \text{m}

Step 3: Work out the percentage growth.

\dfrac{9.01616 - 7.6}{7.6} \times 100 = 18.6\%