Question 1

Between which months did Mercury show the biggest percentage increase in sales?

A: April – May

B: May – June

C: June – July

D: July – August

Written Solutions

Between April and May, sales rose from £160,000 to £180,000. This is a difference of £20,000. Divide this by the original amount and multiply by 100 to work out the percentage increase.

\pounds20,000 \div \pounds160,000 \times 100 = 12.5\% increase

Between May and June, sales rose from £180,000 to £210,000. This is a difference of £30,000. Divide this by the original amount and multiply by 100 to work out the percentage increase.

\pounds30,000 \div \pounds210,000 \times 100 = 16.6\% increase.

Between June and July, sales rose from £210,000 to £240,000. This is a difference of £30,000. Divide this by the original amount and multiply by 100 to work out the percentage increase.

\pounds30,000 \div \pounds210,000 \times 100 = 14.3\% increase

Between July and August, sales rose from £240,000 to £250,000. This is a difference of £10,000. Divide this by the original amount and multiply by 100 to work out the percentage increase.

\pounds10,000 \div \pounds240,000 \times 100 = 4.2\% increase

Therefore, the greatest percentage increase in sales was between May and June.

\pounds270,000 \times 1.15 = \pounds310,500

Question 2

Conquest and Mercury have predicted a 15% increase in sales from August to September, and Pegasus have set a target of a 35% increase in sales from August to September. If these predictions and targets are correct, what will be the combined sales for September for these three companies?

A: £76,525

B: £86,800

C: £765,250

D: £868,000

Written Solutions

If Conquest’s sales increase by 15% from August, then in September they will make: \pounds270,000 \times 1.15 = \pounds310,500

If Mercury’s sales increase by 15% from August, then in September they will make: \pounds250,000 \times 1.15 = \pounds287,500

If Pegasus’s sales increase by 35% from August, then in September they will make: \pounds200,000 \times 1.35 = \pounds270,000

Combined, they will make: \pounds310,500 + \pounds287,500 + \pounds270,000 = \pounds868,000

Question 3

Mercury have a policy of paying an 8% commission to staff on all sales above a monthly target of £180,000. How much commission did Mercury have to pay for the period April to August inclusive?

A: £10,260

B: b) £12,800

C: £16,740

D: £16,800

Written Solutions

First of all, work out how much Mercury made in each month from April to August:

April: £160,000

May: £180,000

June: £210,000

July: £240,000

August: £250,000

Commission is only payable if £180,000 is made in a month, so no commission is payable in either April or May.

The value of sales above the monthly target of £180,000 in June is:

\pounds210,000 - \pounds180,000 = \pounds30,000

The value of sales above the monthly target of £180,000 in June is:

\pounds240,000 - \pounds180,000 = \pounds60,000

The value of sales above the monthly target of £180,000 in June is:

\pounds250,000 - \pounds180,000 = \pounds70,000

The value of total sales above the monthly target is:

\pounds 30,000 + \pounds 60,000 + \pounds 70,000 = \pounds 160,000

8% commission is paid on £160,000 so the total commission payable is:

0.08 \times \pounds 160,000 = \pounds 12,800

Question 4

Pegasus paid a 12% commission to staff for all sales over £260,000 in April.  This was increased to a 16% commission for all sales over £220,000 from May onwards.  What was the difference in commissions paid to staff in April and May?

A: £2,800

B: £3,900

C: £6,400

D: £7,600

Written Solutions

We need to work out how much commission was due to staff in April and how much was paid in May and simply work out the difference.

In April, Pegasus made £330,000 of sales, so if they pay commission on sales over £260,000, then they need to pay commission on £70,000.

Now we need to work out how much the commission was:

0.12 \times \pounds70,000 = \pounds8,400

In May, Pegasus made £290,000 of sales, so if they pay commission on sales over £220,000, then they need to pay commission on £70,000

(\pounds 290,000 - \pounds 220,000 = \pounds 70,000)

Now we need to work out how much the commission was:

0.16 \times \pounds 70,000 = \pounds 11,120

The difference in commission between April and May is:

\pounds 11,200 - \pounds 8,400 = \pounds 2,800

Question 5

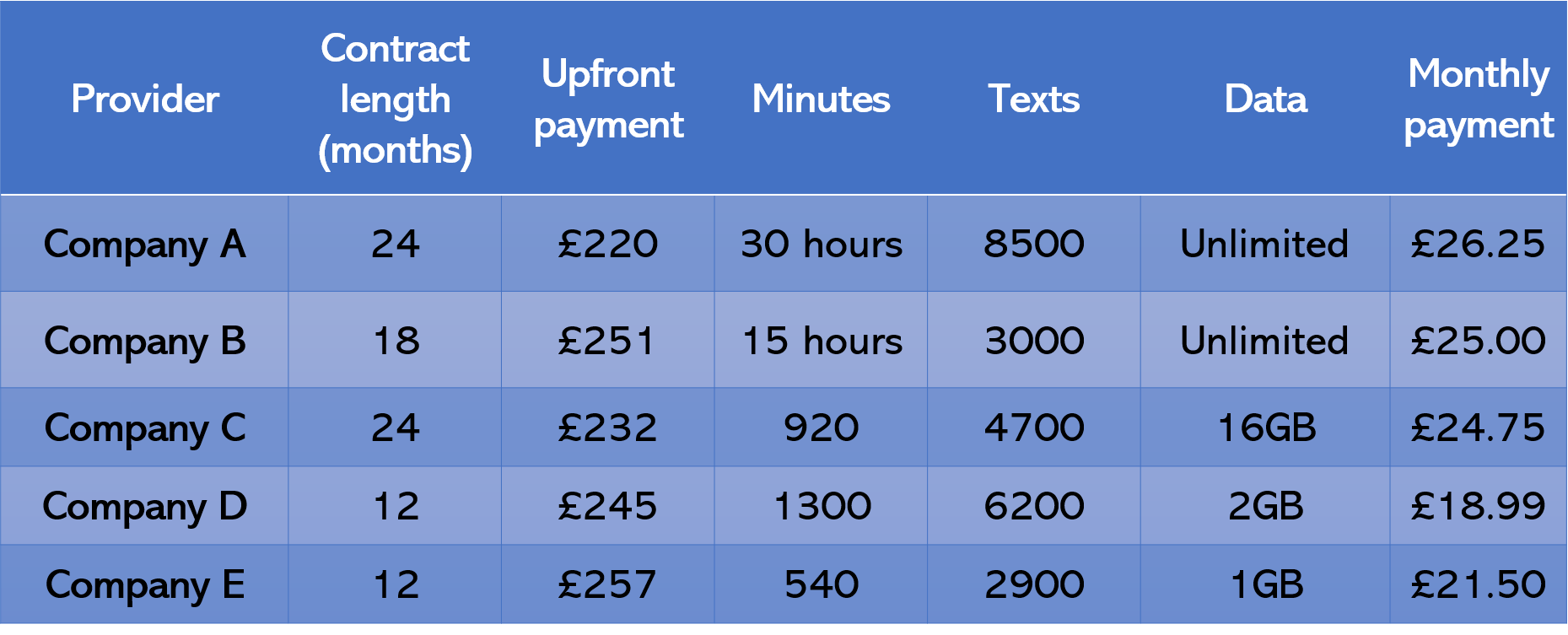
What is the difference in cost between a 12 month contract with Company D and a 12 month contract with company E?

A: £30.12

B: £42.12

C: £485.88

D: £987.88

Written Solutions

The cost of a 12 month contract with Company D is the upfront payment of \pounds245 + (12 \times monthly payment of

\pounds18.99) \pounds245 + (12 \times \pounds18.99) = \pounds 472.88

The cost of a 12 month contract with Company E is the upfront payment of \pounds 257 + (12 \times monthly payment of

\pounds21.50) \pounds257 + (12 \times \pounds21.50) = \pounds515.00

The difference between them is:

\pounds515 - \pounds472.88 = \pounds42.12

Question 6

Monthly rates are due to increase by 4% per year for the next two years due to inflation.  To the nearest penny, what will be the total cost of a two year contract with Company A (including the upfront payment) taking these annual increases into consideration?

A: £540.70

B: £830.00

C: £855.20

D: £888.30

Written Solutions

The monthly fees for company A are £26.25 per month. If they are going to increase by 4% in the following year then the new monthly rate will be:

\pounds 26.25 \times 1.04 = \pounds27.30

Therefore the annual rate will be:

\pounds 27.30 \times 12 = \pounds 327.60

The following year, the fees will again increase by 4% from £327.60, so the fees for the following year will be:

\pounds 327.60 \times 1.04 = \pounds 340.70

Therefore the price of a 2 year contract, including the upfront payment, will be:

\pounds 220 + \pounds 327.60 + \pounds 340.70 = \pounds 888.30

Question 7

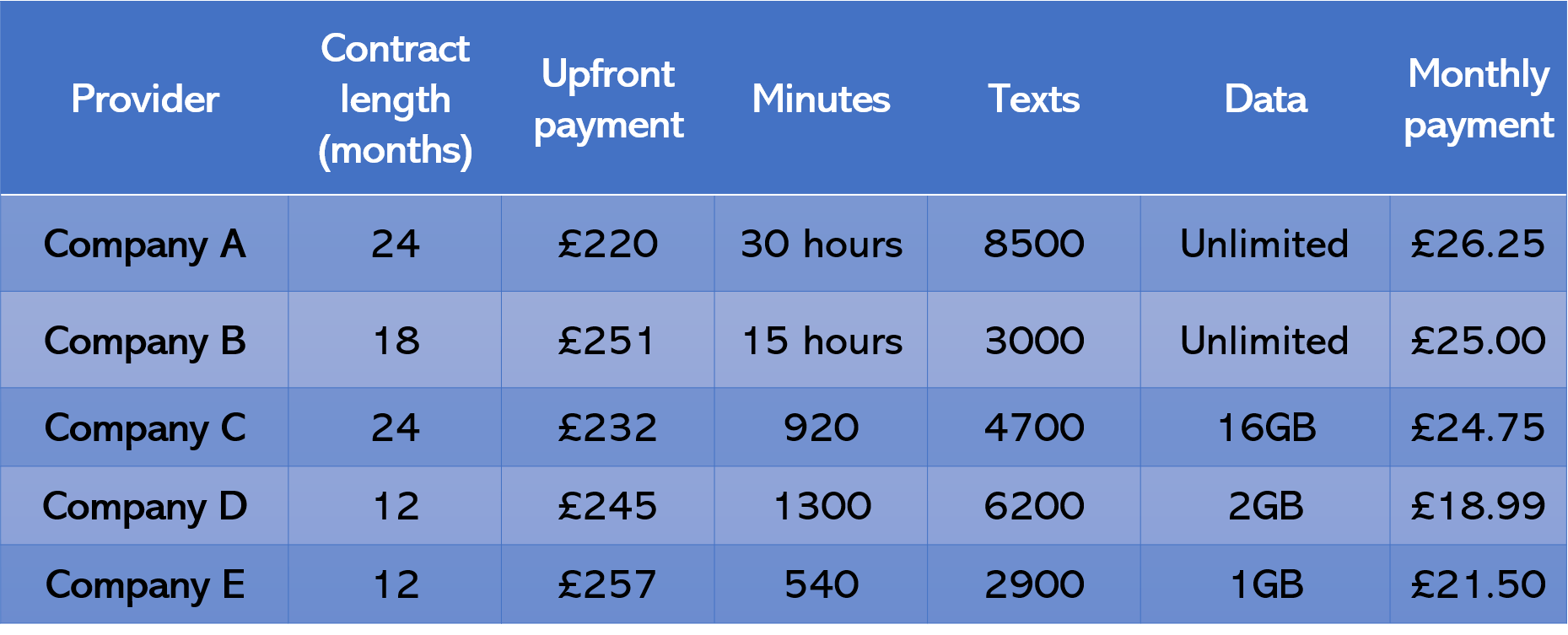
Three brothers, Steve, Gary and Wayne, share a phone on a contract with Company C and use data in the ratio of  5 : 7 : 11.  Over three months,  Steve used 20GB.  Additional data is charged at £2.25 per 1GB.  If the cost of the additional data is shared equally between the 3 brothers, and assuming that they exceeded their allowance in all 3 months, how much do they have to pay each for the additional data used if they share the cost of the extra data equally?

A: £22.50

B: £33

C: £46

D: £135

Written Solutions

The ratio of Steve : Gary : Wayne is 5 : 7 : 11. Steve used 20 GB which is 4 times more than the figure in his ratio share.

Therefore Gary used 7 \times 4 = 28 \text{ GB} and Wayne used 11 \times 4 = 44\text{ GB}.

In total, they used 20\text{ GB} + 28\text{ GB} + 44\text{ GB} = 92\text{GB of data.}

Over the three month period, they would have had an allowance of 16\text{ GB}\times 3 = 48\text{ GB}, so they will be charged for

92\text{ GB used} – 48\text{ GB allowance} = 44\text{ GB}

Additional data is charged at £2.25 per GB, so the total chargeable amount is:

44\text{ GB}\times \pounds2.25 = \pounds 99

If this is split three ways, then each brother will have to pay £33.

Question 8

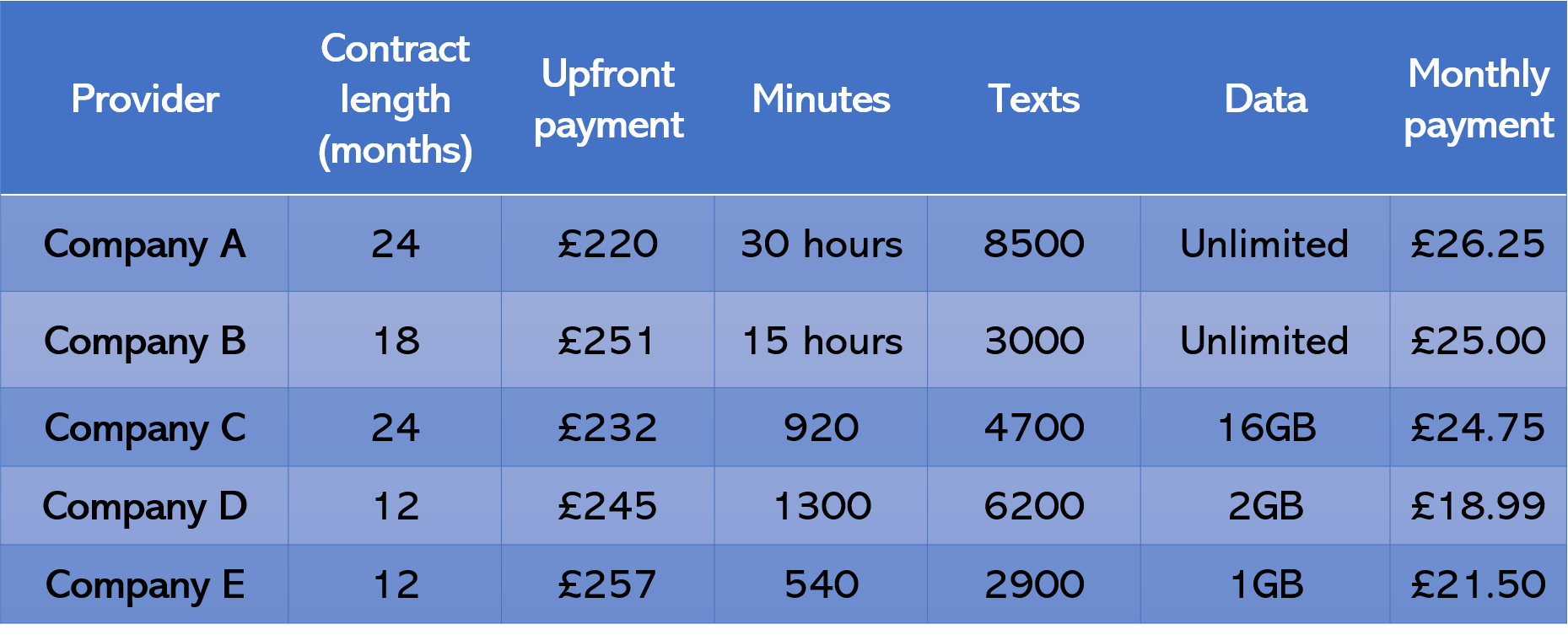
Company C charge an additional 32p per minute for any calls that are outside of the monthly allowance.  If a user uses 20 hours per month, how much would he save if the user started a 2 year contract with Company A instead of starting a two year contract with Company C?

A: £2150.40

B: £2126.40

C: £2162.40

D: £2186.40

Written Solutions

If a user uses 20 hours per month, that is a total of 20 \times 60 minutes = 1200 minutes.

If the monthly allowance is 920 minutes, then the user has exceeded the limit by 1200 - 920 minutes = 280 minutes.

If the fee is 32p per minute, then the user has accrued an additional 280 \times 32p of additional costs = \pounds89.60 per month.

With Company C, the user will pay an upfront payment of £232, 24 times the monthly fee of £24.75 and 24 times the additional phone charges of £89.60:

\pounds 232 + (24 \times \pounds 24.75) + (24 \times \pounds 89.60) = \pounds 2976.40

If the user had used Company A, over a 2-year period, he would have been charged:

\pounds 220 + (24 \times \pounds26.25) = \pounds 850

Had the user used Company A, he would have saved \pounds 2976.40 - \pounds 850 = \pounds 2126.40

Question 9

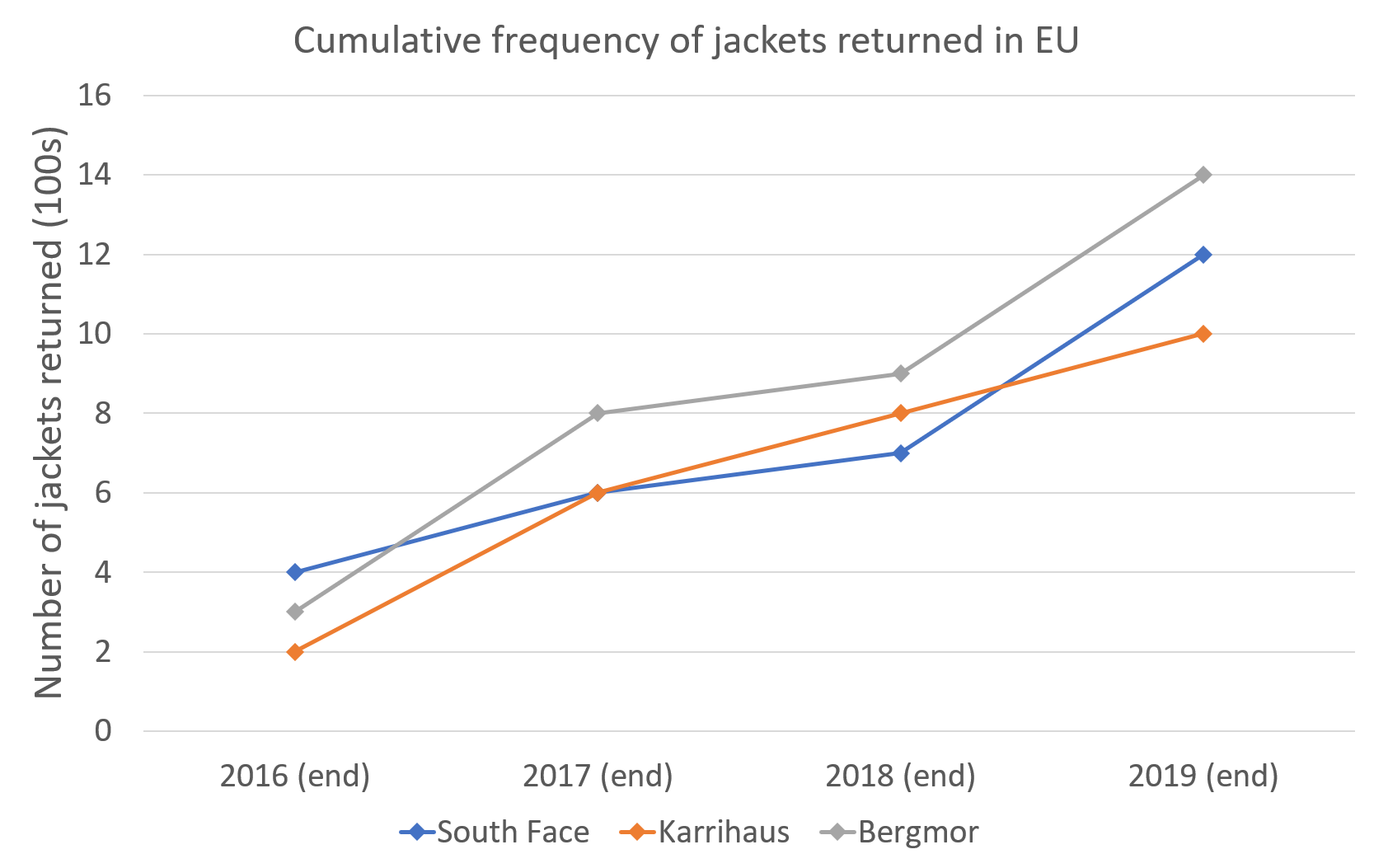
How many jackets were returned to South Face between the end of 2017 and 2019?

A: 600

B: 800

C: 2500

D: 2800

Written Solutions

Since this is a cumulative frequency graph, we simply need to subtract the end of 2017 sales from the end of 2019 sales for South Face:

1200 - 600 = 600 jackets

Question 10

Of the 3 jacket companies combined, between which years was there the biggest percentage increase in the number of returned jackets?

A: 2016 – 2017

B: 2017 – 2018

C: 2018 – 2019

D: Impossible to determine from the data provided

Written Solutions

This question is much harder than it seems. Remember that this is a cumulative frequency graph and not a regular graph. The total number of jackets returned in any given year cannot be read directly from the graph; you need to deduct all previous returns from the given values.

In 2016, there were 900 jackets returned.

In 2017, there were 2000 - 900 = 1100 jackets returned.

In 2018, there were 2400 - 2000 = 400 jackets returned.

In 2019, there were 3600 - 2400 = 1200 jackets returned.

Between 2016 and 2017, jacket returns increased some 900 to 1100. As a percentage increase, this would be:

\dfrac{1100 - 900}{900} = 22.2\% increase

Between 2017 and 2018, jacket returns decreased, so there is no value in calculating this part.

Between 2018 and 2019, jacket returns increased from 400 to 1200. As a percentage increase, this would be:

\dfrac{1200 - 400}{400} = 200\% increase

Therefore, the biggest percentage increase in jacket returns was between 2018 and 2019.

Question 11

Given that the data in the table has been rounded to the nearest hundred, what was the minimum number of jackets returned to Bergmore between the end of 2016 and the end of 2019?

A: 880

B: 975

C: 1050

D: 1100

Written Solutions

Between 2016 and 2019, there were 1100 returned jackets. If this has been rounded to the nearest hundred and we are looking the minimum possible number of jackets that were returned, we are looking for the lowest number that would round up to 1100 and not down to the next lowest hundred (which would be 1000). 1050 is the lowest number that rounds up to 1100 and not down to 1000.

Question 12

Typically, the number of returns from South Face in North America is 25% more than in the EU and the number of returns in Asia is 10% more than the number of returns in North America. How many jackets were returned from North America and Asia combined up to the end of 2019?

A: 1645

B: 2060

C: 3150

D: 3640

Written Solutions

In the EU, the total number of jackets returned up to the end of 2019 was 1200. If the number of returns in North America was 25% more, then the number of jackets returned in North America was:

1200 \times 1.25 = 1500 jackets

The number of returns in the Asian market was 10% more than the number of returns in the North American market, so the number of jackets returned in the Asian market was:

1500 \times1.1 = 1650 jackets

Therefore, the total number of jackets returned from North America and Asia combined was:

1650 + 1650 = 3150 jackets

Question 13

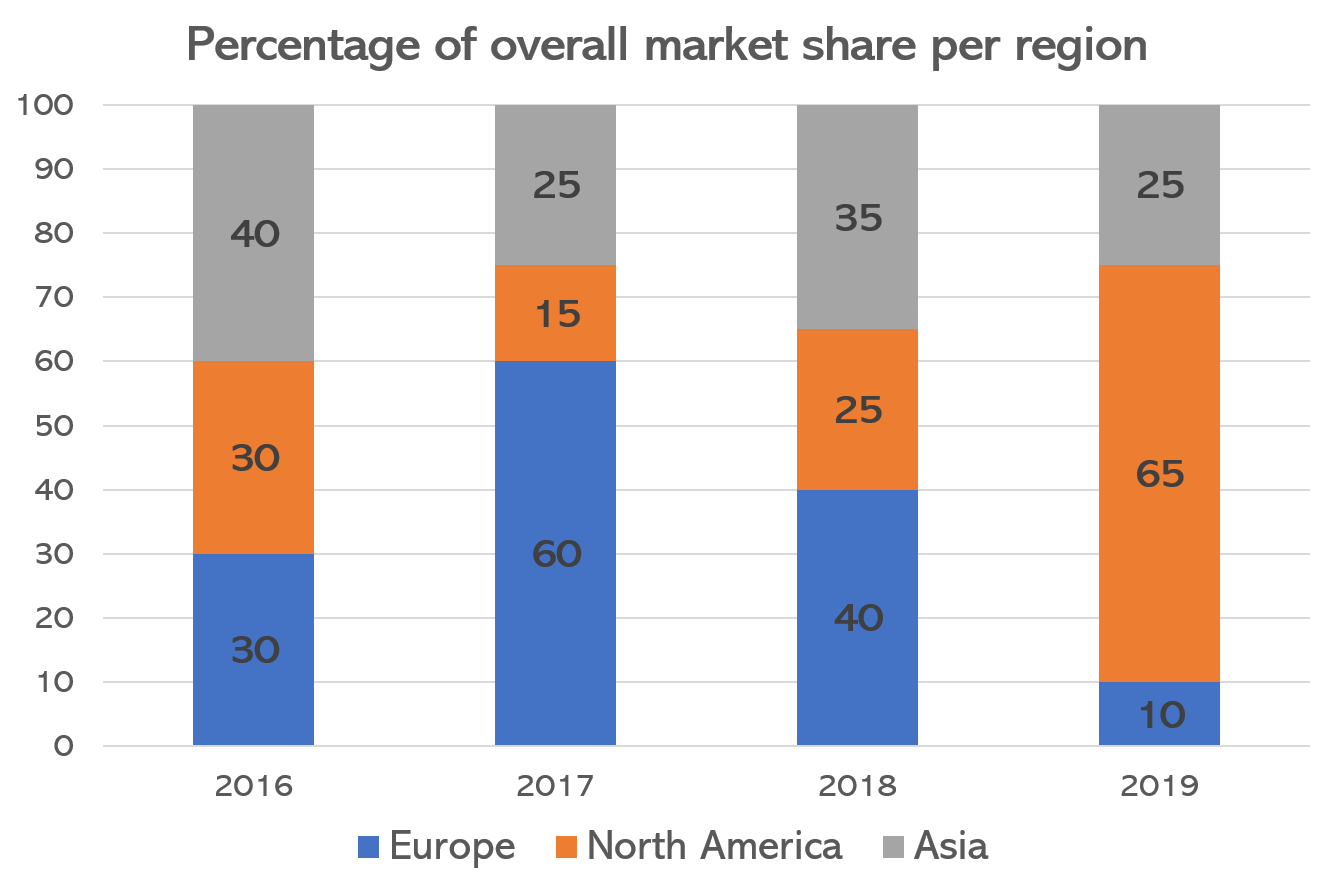
The total market share in 2016 was £1.6 billion and in 2017 it was £2.3 billion.  What was the difference between the market share of the Asian sector between 2016 and 2017?

A: £8,500,000

B: £65,000,000

C: £650,000,000

D: £8,500,000,000

Written Solutions

In 2016, the Asia sector comprised 40% of the overall market share which had a value of £1.6 billion, so the value of the Asia sector was:

\pounds 1.6 billion \times 0.4 = \pounds 0.64 billion

In 2017, the Asia sector comprised 25% of the overall market share which had a value of £2.3 billion, so the value of the Asia sector was:

\pounds 2.3 billion \times 0.25 = \pounds 0.575 billion

Therefore, the difference between 2017 and 2016 was:

\pounds 0.64 billion - \pounds 0.575 billion = \pounds 0.065 billion

\pounds 0.065 billion = \pounds 65,000,000

Question 14

The total market share in 2018 was £5.3 billion.  The Europe sector’s market share is generated by Italy, France and Germany whose individual market shares are in the ratio of 1:4:3.  What is the value of Germany’s market share?

A: £525,000,000

B: £645,000,000

C: £795,000,000

D: £825,000,000

Written Solutions

If the total market share in 2018 was £5.3 billion and the European sector comprised 40% of this, then the total value of the European sector was:

\pounds 5.3 billion \times 0.4 = \pounds 2.12 billion

If the ratio of Italy : France : Germany was 1 : 4 : 3, then Germany’s share was \frac{3}{8} of \pounds 2.12</p> <p> billion. (We are dealing in eighths since the sum of the ratio is 8.)

Therefore, Germany’s share was:

\pounds 2.12 \times \frac{3}{8} = \pounds 0.795 billion or \pounds 795,000,000

Question 15

The total market share in 2019 was £3.7 billion.  It is predicted that the total market share will increase by 2.5% in 2020.  If the three regions have the same percentage share in 2020 as they do in 2019, what will be the value of the North American sector in USD given an exchange rate of $1.36 = £1.00?

A: $2,784,100,000

B: $3,352,570,000

C: $4,689,340,000

D: $4,893,880,000

Written Solutions

If the total market share in 2020 is 2.5% more than 2019, which itself has a value of £3.7 billion, then the vale of the total market share in 2020 will be:

\pounds 3.7 billion \times 1.025 = \pounds 3.7925 billion

The North America share remains at 65%, so the value of the North America share will be:

\pounds 3.7925 billion \times 0.65 = \pounds 2.465125 billion

If this is the amount in pounds, we simply need to convert this from pounds to dollars.

\pounds 465,125 billion \times \$1.36 = \$3.35257 or \$3,352,570,000

Question 16

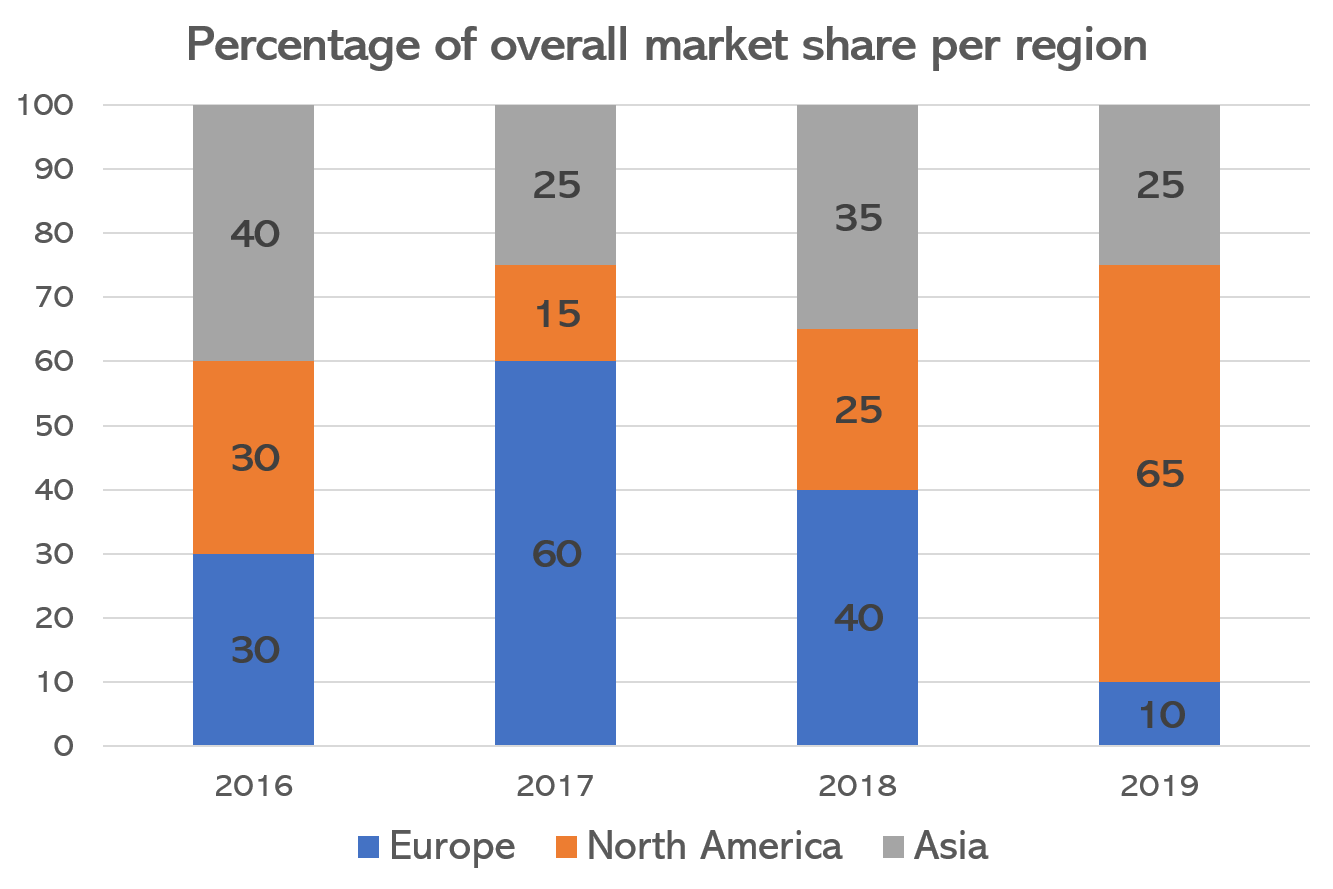
The total market share in 2019 was £3.7 billion. In 2020 the Asian market share will have a value of 170 billion Japanese Yen which represents 20% of the total market share.  Given this information, what is the percentage increase in value of the overall market share from 2019 to 2020?  The exchange rate is £1.00 = 150 Japanese Yen.

A: 18%

B: 36%

C: 53%

D: 62%

Written Solutions

If in 2020, the Asian market represents 20% of the total market share and has a value of 170 billion Japanese Yen, then the overall market share will have a value of:

170 billion Yen \div 20 \times 100 = 850 billion Yen

850 billion Yen in British pounds is:

850 billion Yen \div 150 Yen = \pounds 5.\dot{6} billion

If the overall market share has increased from £3.7 billion to £5.\dot{6} billion, then as a percentage increase this would be:

\dfrac{\pounds 5.\dot{6}\text{ billion} - \pounds 3.7 \text { billion}}{\pounds 3.7 \text{ billion}}\times 100 = 53.15\% (53\% to the nearest percentage)

Question 17

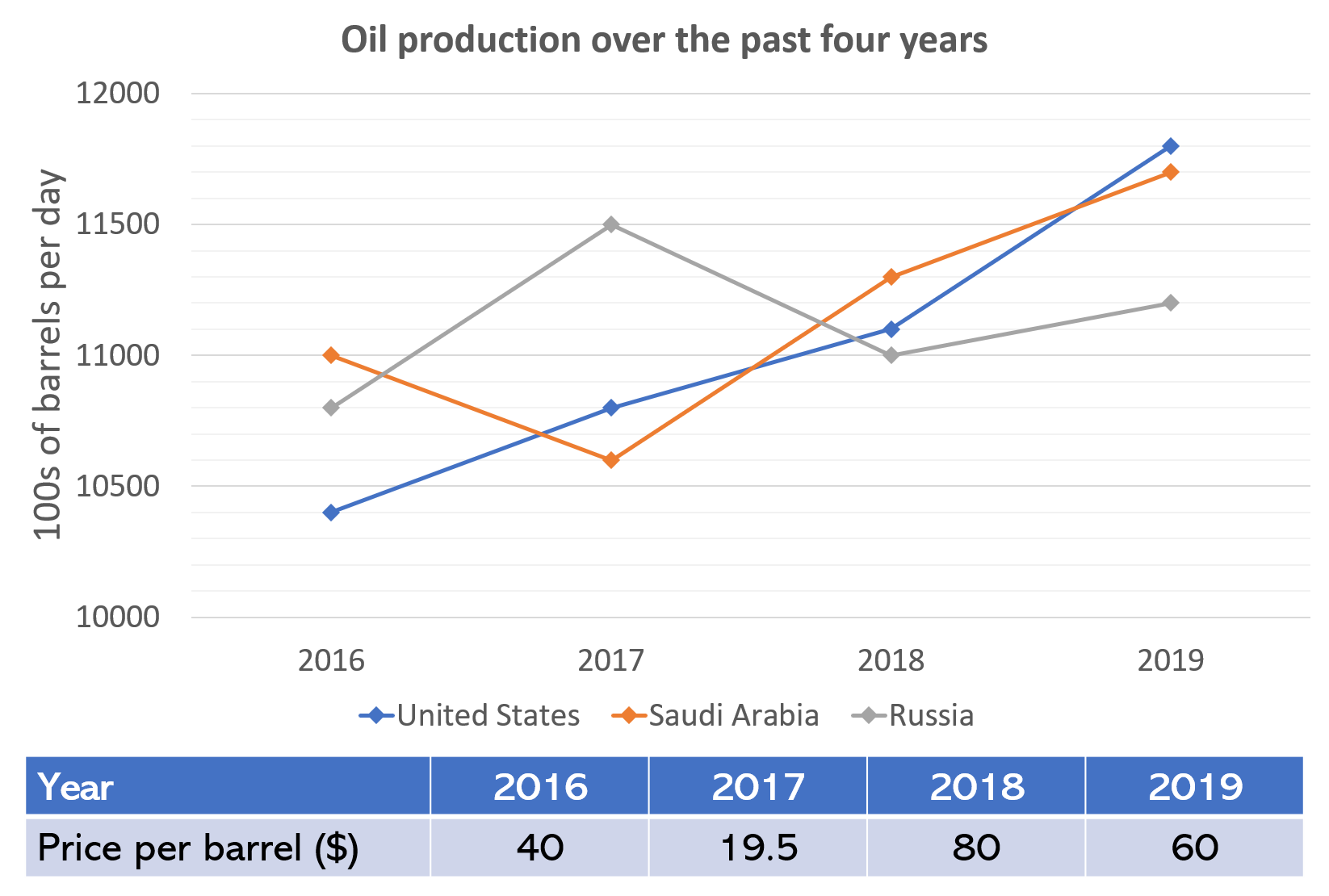
What was the percentage increase in the number of barrels of oil produced between 2016 and 2019 of the three countries combined?

A: 5.43%

B: 7.76%

C: 8.49%

D: 12.62%

Written Solutions

In 2016, the 3 countries produced 10,400, 10,800 and 11,000 barrels, although this is hundreds of barrels. However, since we are working out a percentage increase, we don’t need to multiply these numbers by 100, provided we do the same with the 2019 values.

In total, the 3 countries produced 10,400 + 10,800 + 11,000 = 32,200 hundreds of barrels.

In 2019, the three countries produced 11700 + 11,800 + 11,200 = 34,700 hundreds of barrels.

As a percentage increase this needs to be calculated as follows:

(34,700 - 32,200) \div 32,200 \times 100 = 7.76\%

Question 18

What was the value of the oil generated in 2017 by Saudi Arabia?

A: $132,450,000

B: $20,670,000

C: $1.3245 billion

D: $7.54455 billion

Written Solutions

In 2017, Saudi Arabia produced 10,600 hundreds of barrels per day, therefore they produced 10,600 \times 100 = 1,060,000 barrels per day and 1,060,000 \times 365 = 386,900,000 barrels in the year.

If the oil is priced as $19.50 per barrel, then the value of the oil is 386,900,000 \times \$19.50 = \$7,544,550,000 = \$7.54455 billion.

Question 19

What percentage of the total number of barrels of oil produced by Russia was produced by Russia in 2017?

A: 25.8%

B: 32.4%

C: 36.7%

D: 39.4%

Written Solutions

In 2017, Russia produced 11,500 hundreds of barrels of oil. In total, the number of barrels of oil produced by Russia over this four-year period was 10,800 + 11,500 + 11,000 + 11,200 = 44,500 hundreds of barrels of oil.

Again, since we are dealing with percentages, it is easier to leave the numbers as they are and deal with ‘hundreds of barrels of oil’ as the unit rather than converting to barrels of oil (e.g. leave a figure as 10,800 hundreds of barrels of oil than convert it to 1,080,000 barrels of oil).

The percentage the Russia produced in 2017 was:

11,500 \div 44,500 \times 100 = 25.8\%

Question 20

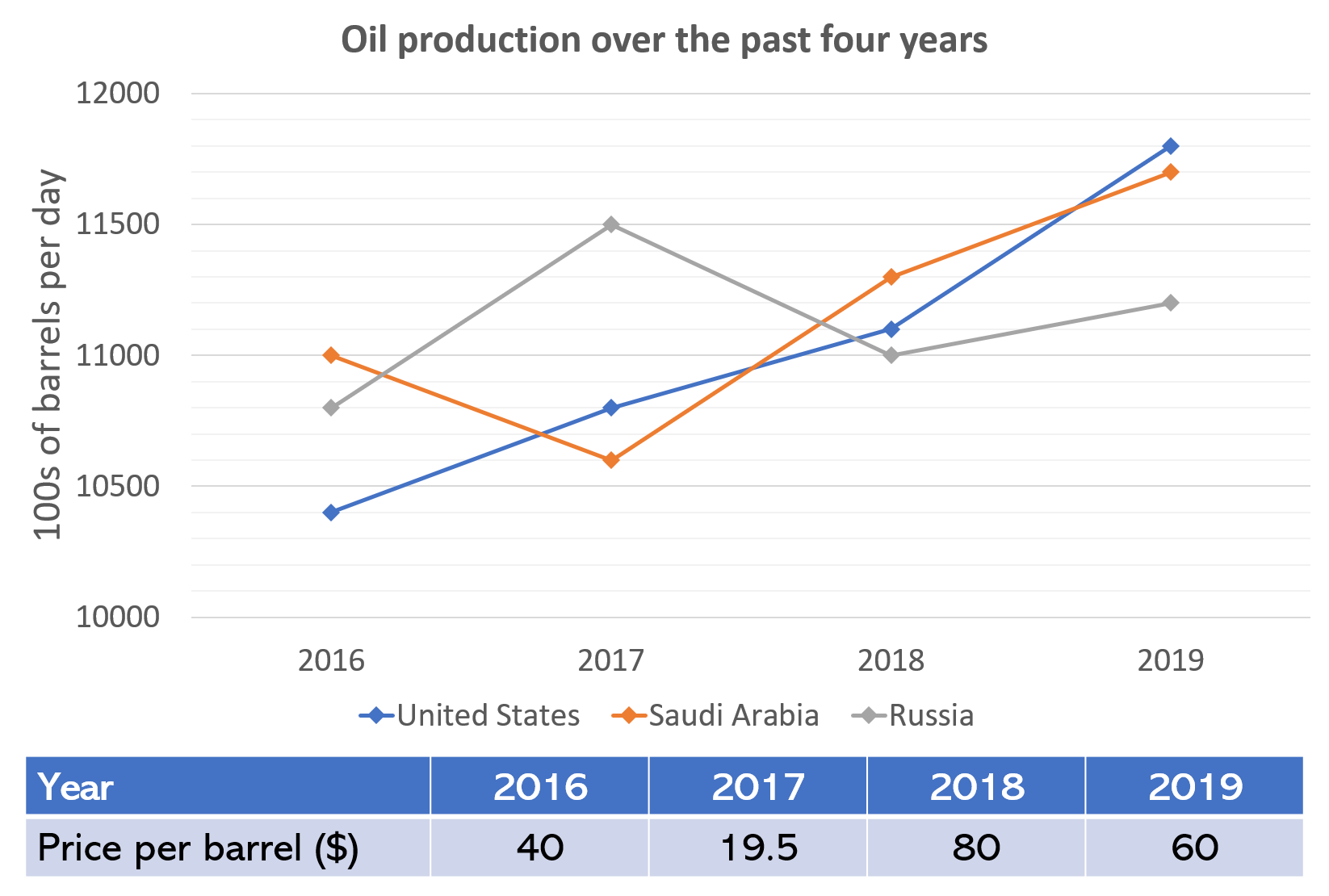
Assuming that the price of oil falls at the same percentage rate between 2019 and 2020 as it did between 2018 and 2019, what will be the value of the oil produced per day by Russia in 2020 if Russia increases its daily production by 10% from 2019?

A: $55,440,000

B: $58,410,000

C: $61,200,000

D: $68,200,000

Written Solutions

In 2018, the price of oil was $80 and fell to $60 in 2019. As a percentage decrease, this is:

\dfrac{(\$80 - \$60)}{\$80}\times 100 = 25\% decrease

If the value of oil drops again by this percentage, then the value of a barrel of oil in 2020 will be:

\$60 \times 0.75 = \$45

Russia produced 11,200 hundreds of barrels in 2019, so if it increases its production by 10% in 2020, then Russia will produce:

11,200 \times 1.1 = 12,230 hundreds of barrels of oil = 1,232,000 barrels of oil.

The total value of the oil produced will therefore be:

1,232,000 \times \$45 = \$55,440,000