Question 1

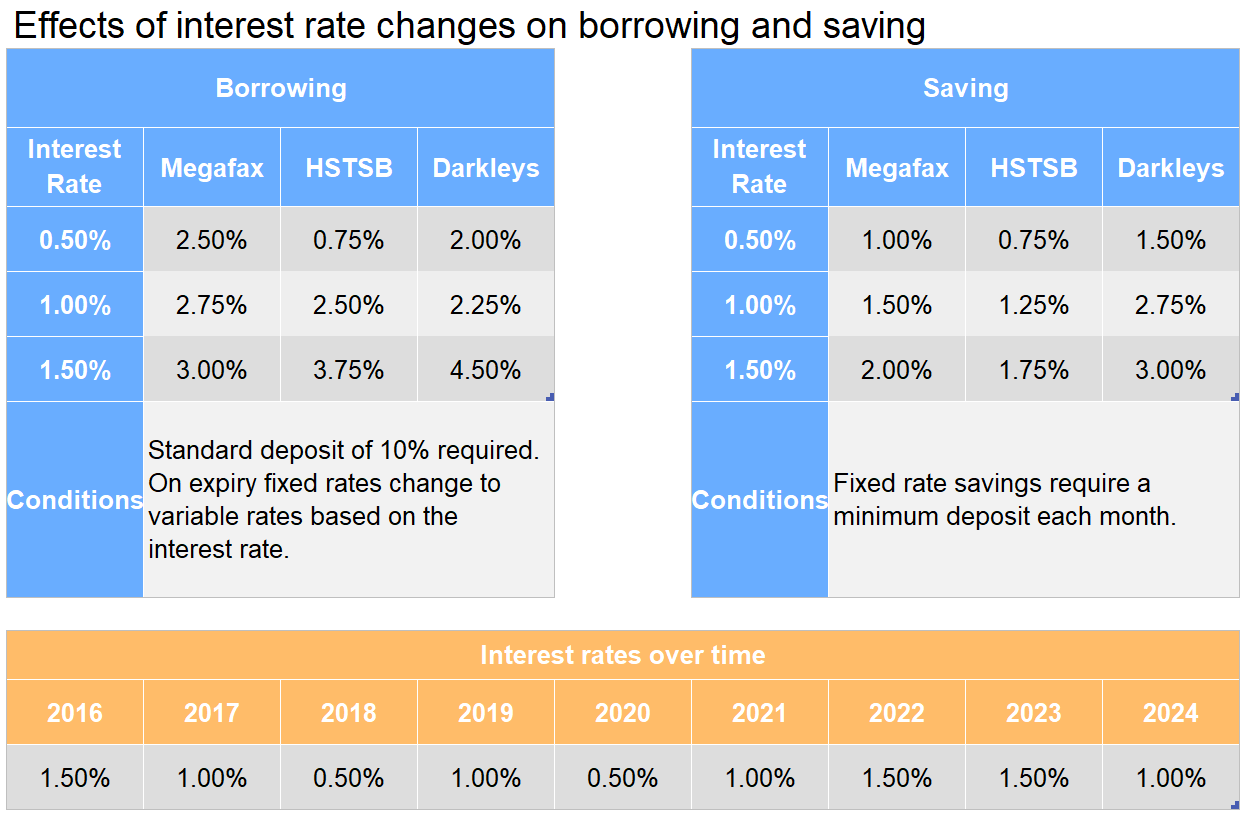
A customer takes 2 fixed rate loans from Megafax, borrowing £4,000 and £12,000 separately, starting in 2018. They repay part of the loans each year in the ratio 1: 6, with £3,500 repaid in total in year 1. What is the ratio of the amounts to be repaid at the end of year 4?

A: 4.8: 1

B: 4.7: 1

C: 4.6: 1

D: 4.5: 1

Written Solutions

Step 1: Calculate the actual value of monies repaid in year 1. 1: 6 is 7 parts total. Divide the total amount of money by 7 to find the value of one share.

\pounds3,500 \div 7 = \pounds500

Now multiply the ratio by £500 to find the actual ratio of monies that were repaid.

1:6 \times 500 \equiv \pounds500: \pounds3,500

Step 2: For the first loan, assume £500 repaid and then an increase of 2.5% due to the fixed interest rate. This is a multiplier of 1.025.

(\pounds4,000-\pounds500)\times1.025=\pounds3,587.50

Now repeat this for the next three years.

(\pounds3,587.50-\pounds500)\times1.025=\pounds3,164.69

(\pounds3,164.69-\pounds500)\times1.025=\pounds2,731.31

(\pounds2,731.31-\pounds500)\times1.025=\bold{\pounds2,287.09}

Step 3: Make the same calculation but for the larger loan.

(\pounds12,000-\pounds3,000)\times1.025=\pounds9,225

(\pounds9,225-\pounds3,000)\times1.025=\pounds6,380.63

(\pounds6,380.63-\pounds3,000)\times1.025=\pounds3,465.14

(\pounds3,465.14-\pounds3,000)\times1.025=\bold{\pounds476.77}

Step 4: Form and simplify the ratio

\begin{gathered}\pounds2,287.09: \pounds476.77 \\ \dfrac{2,287.09}{476.77}: 1 \\ \bold{4.8: 1}\end{gathered}

Question 2

What is the difference after three years between saving £3,000 paid yearly into a fixed rate Darkleys account or £9,000 paid immediately into a variable account, starting in 2016. Give your answer to the nearest pound.

A: £111

B: £114

C: £117

D: £120

Written Solutions

Step 1: Calculate the total after three years for the variable rate £9,000. The savings rates for this period are 3%, 2.75%, and 1.5%. These correspond to multipliers of 1.03, 1.0275 and 1.015 respectively.

\pounds9,000\times1.03\times1.0275\times1.015 = \pounds9,667.80

Step 2: The calculation for the fixed rate loan is more complex, the savings rate is 3%, or a multiplier of 1.03. For the first year, interest is earned on the first deposit of £3,000.

\pounds3,000\times1.03=\pounds3,090

Next add £3,000 on to this and calculate interest again, and then one more time.

(\pounds3,090+\pounds3,000)\times1.03=\pounds6,272.70

(\pounds6,272.70+\pounds3,000)\times1.03=\pounds9,550.88

Step 3: So, the difference in savings is

\pounds9,667.80-\pounds9,550.88\approx\bold{\pounds117}

Question 3

£30,000 is saved in a Megafax variable account from 2016. In 2024, what proportion of the initial savings have been gained due to interest? Give your answer to 1dp.

A: 14.6%

B: 14.7%

C: 14.8%

D: 14.9%

Written Solutions

Step 1: The savings rates over these years and their corresponding multipliers are:

2\% \equiv 1.02\text{ and three occurrences is }1.02^3

1.5\% \equiv 1.015\text{ and four occurrences is }1.015^4

1\% \equiv 1.01\text{ and two occurrences is }1.01^2

Step 2: Use these multipliers to calculate the total amount in the account in 2024, and subtract £30,000 to find the total accrued due to interest.

\pounds30,000\times1.02^3\times1.015^4\times1.01^2=\pounds34,469

\pounds34,469-\pounds30,000=\pounds4,469

Step 3: Calculate the proportion of the initial value.

\dfrac{4,469}{30,000}\times100=\bold{14.9\%}

Question 4

If no repayments are required, what is the lowest total value to be repaid in 2024 on a £25,000 loan that is at a fixed rate for 5 years starting in 2016? Give your answer to the nearest pound.

A: £28,450

B: £29,215

C: £30,588

D: £32,013

Written Solutions

Step 1: A deposit of 10% must be made so the loan is on a value of 0.9\times\pounds25,000=\pounds22,500. Make the calculation for Megafax. A fixed rate in 2016 starts at 3% and then reverts to the variable rate in 2021. This is 5 years at 3%, then two years of 2.75% and two more of 3%.

\pounds22,500\times1.03^7\times1.0275^2=\pounds29,215.06

Step 2: Make the same calculation for HSTSB, in this case the corresponding rates are 3.75% for 7 years and 2.5% for two years.

\pounds22,500\times1.0375^7\times1.025^2=\pounds30,587.71

Step 3: Make the same calculation for Darkleys, and then conclude which is best value. The rates are 4.5% for 7 years and 2.25 for two years.

\pounds22,500\times1.045^7\times1.0225^2=\pounds32,012.76

Megafax was best value for a total of approximately £29,215.

Question 5

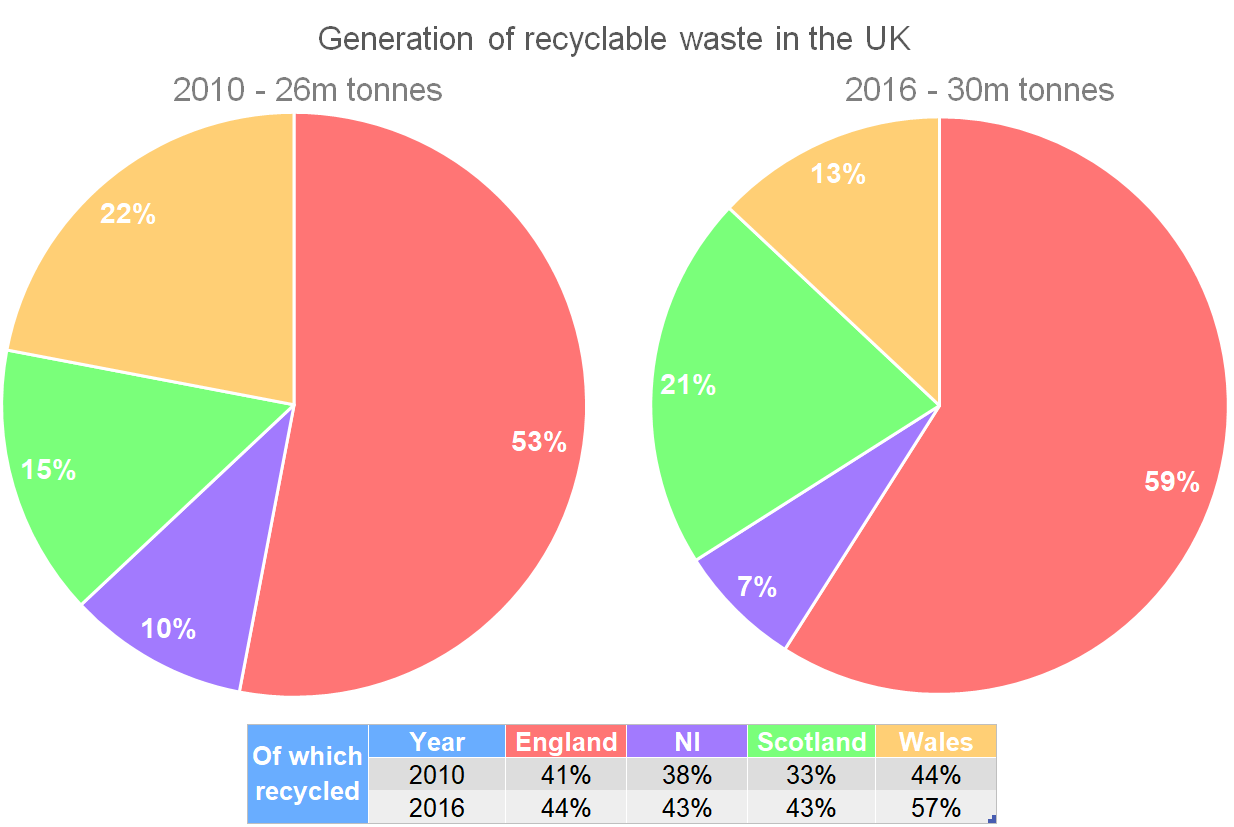
What is the percentage increase in quantity of waste that was recycled in England between 2010 and 2016? Give your answer to 1dp.

                A: 37.8%

B: 38.2%

C: 38.6%

D: 39.0%

Written Solutions

Step 1: Calculate the quantity that was recycled in 2010. First find the quantity of waste for 2010. This is 53% of 26m, or a multiplier of 0.53.

0.53 \times 26 = 13.78\text{m tonnes}

We are told that 41% of this was recycled which is a multiplier of 0.41.

0.41\times13.78=5.6498\text{m tonnes recycled}

Step 2: Make the same calculation for 2016.

0.59\times30=17.7\text{m tonnes}

0.44\times17.7=7.788\text{m tonnes recycled}

Step 3: Find the percentage increase from 2010 to 2016.

\dfrac{7.788-5.6498}{5.6498}\times100=\bold{37.8\%}

Question 6

What is the ratio of waste recycled for the UK in 2010. Give your answer in its simplest form for England: NI: Scotland: Wales, and to 1dp.

A: 5.9: 1: 1.5: 2.9

B: 5.4: 1: 1.4: 2.7

                C: 5.7: 1: 1.3: 2.5

D: 5.1: 1: 1.1: 2.3

Written Solutions

Step 1: First calculate the amount of recyclable waste for each part of the UK.

\begin{aligned}\text{England: }&0.53\times26=13.78\text{m} \\ \text{NI: }&0.1\times26=2.6\text{m} \\ \text{Scotland: }& 0.15\times26=3.9\text{m} \\ \text{Wales: }& 0.22\times26=5.72\text{m}\end{aligned}

Step 2: Now multiply each of these to calculate the amount actually recycled in the UK in 2010.

\begin{aligned}\text{England: }&13.78\times0.41=5.6498 \\ \text{NI: }&2.6\times0.38=0.988 \\ \text{Scotland: }&3.9\times0.33=1.287 \\ \text{Wales: }&5.72\times0.44=2.5168 \end{aligned}

Step 3: Form the ratio and simplify by dividing through by the smallest value.

5.6498: 0.988: 1.287: 2.5168

\dfrac{5.6498}{0.988}: 1: \dfrac{1.287}{0.988}: \dfrac{2.5168}{0.988}

\bold{5.7: 1: 1.3: 2.5}

0.96 \times \pounds1,418k \approx \bold{\pounds1,361k}

Question 7

What is the highest increase in the weight of recyclable waste from 2010 to 2016 between Scotland and England?

A: England – 3.92m

B: England – 4.64m

C: Scotland – 3.44m

D: Scotland – 4.36m

Written Solutions

Step 1: Calculate the change in recyclable waste for Scotland.

(0.21\times30)-(0.15\times26)=2.4\text{m tonnes}

Step 2: Calculate the change in recyclable waste for England.

(0.59\times30)-(0.53\times26)=3.92\text{m tonnes}

Step 3: So, the highest increase is 3.92m tonnes for England.

Question 8

What was the total weight of all waste recycled in the UK in 2016?

A: 12.897m tonnes

B: 13.623m tonnes

C: 13.278m tonnes

D: 13.456m tonnes

Written Solutions

Step 1: First calculate the weight of recyclable waste for each part of the UK.

\begin{aligned}\text{England: }&0.59\times30=17.7\text{m} \\ \text{NI: }&0.07\times30=2.1\text{m} \\ \text{Scotland: }& 0.21\times30=6.3\text{m} \\ \text{Wales: }&0.13\times30=3.9\text{m}\end{aligned}

Step 2: Next use these figures to find out the weight of waste recycled for each area.

\begin{aligned}\text{England: }&0.44\times17.7=7.788\text{m} \\ \text{NI: }&0.43\times2.1=0.903\text{m} \\ \text{Scotland: }&0.43\times6.3=2.709\text{m} \\ \text{Wales: }&0.57\times3.9=2.223\text{m}\end{aligned}

Step 3: Add up the above to find the total amount of waste recycled.

7.788+0.903+2.709+2.223=\bold{13.623\text{m tonnes}}

Question 9

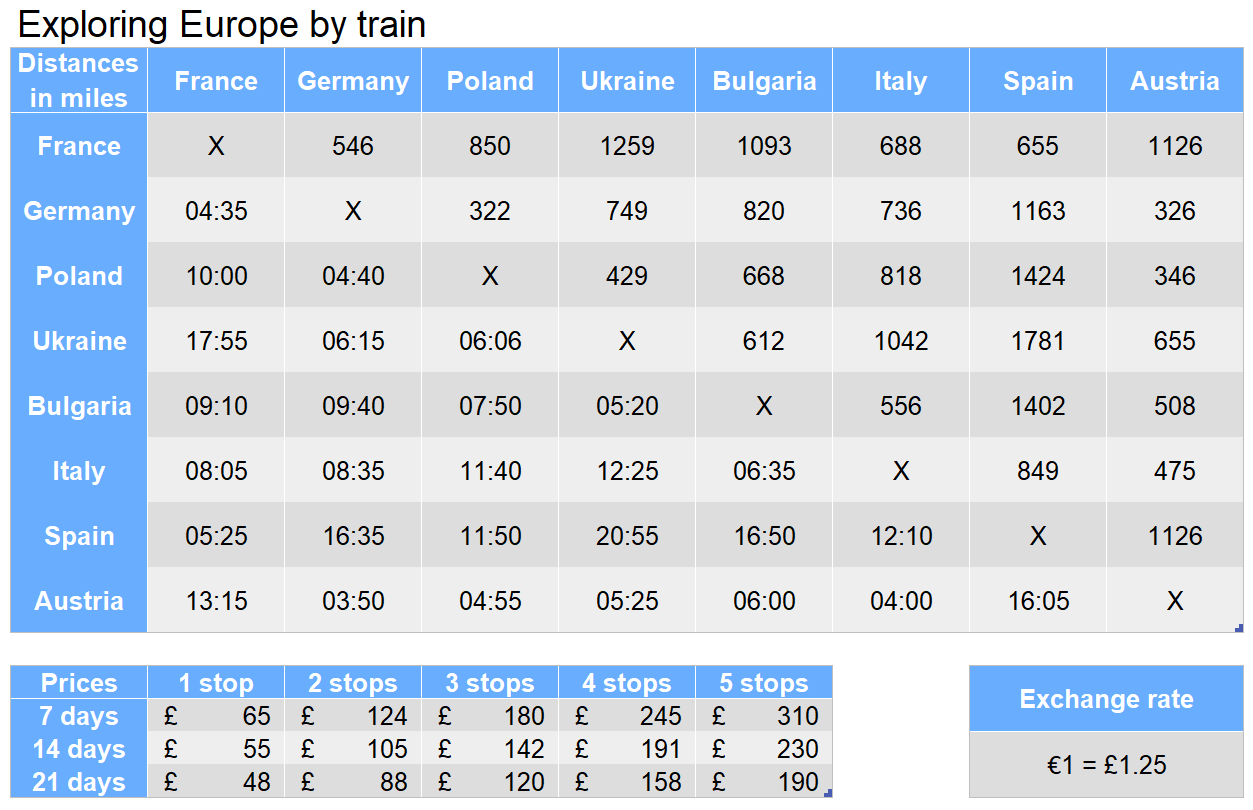
A tourist makes a journey that starts in Germany and visits the following countries in order: Ukraine, Bulgaria, Italy and Austria on a 14-day ticket. What is the average cost per hour spent on the train, if the tourist opts for a 1^st class upgrade for a 45% increase in the ticket cost.

A: £12.24

B: £12.29

C: £12.35

D: £12.49

Written Solutions

Step 1: Add up the time spent on trains between these locations and convert it to a decimal. This is 22:10, so to convert to a decimal divide the minutes by 60:

22:10 \equiv 22+ (10/60)=22.16…

Step 2: Now select the correct cost for this trip of 4 stops and increase it by 45%. This is a multiplier of 1.45.

\pounds191\times1.45=\pounds276.95

Step 3: Divide the total cost by the number of hours to get the average cost per hour.

\pounds276.95 \div 22.16… = \pounds12.49\text{ per hour}

Question 10

3 friends go on a 7-day 4 stop trip. They each have £500 and €400 to spend, which needs to cover the cost of their tickets and general spending. They each spend roughly £80 per day on their trip. How much do they have remaining in total at the end of the trip, in euros?

A: €455

B: €468

C: €449

D: €474

Written Solutions

In total they have £1500 and €1200 euros. The cost of their tickets first needs to be deducted.

\pounds1500-(\pounds245\times3)=\pounds765

Now subtract the spending costs of £80 per person per day.

\pounds765-(80\times7\times3)=-\pounds915

So, the amount in pounds at the beginning of the trip does not cover this. We need to subtract £915 from €1200. Convert the pounds into euros.

915 \div 1.25 = 732\text{ euros}

Finally subtract this from the total amount given in euros.

1200-732=\bold{468\text{ euros}}

Question 11

What is the smallest amount of time that would be spent on trains if I want to start a trip in Austria, visit two other countries, and return to Austria?

A: 13:25

B: 13:30

C: 13:35

D: 13:40

Written Solutions

By inspecting the grid and with some trial and error we identify that the route Austria – Germany – Poland – Austria is the shortest route that achieves this requirement. The total time spent on trains for this is:

03:50+04:40+04:55=\bold{13:35}

Question 12

Which journey, starting in Bulgaria and going to either France, Germany, Poland or Ukraine, has the highest speed train?

                A: France

                B: Germany

                C: Poland

                D: Ukraine

Written Solutions

Step 1: Find the journey times and distances from the grid.

\begin{aligned}\text{France: }&09:10\text{ and }1093\text{ miles} \\ \text{Germany: }&09:40\text{ and }820\text{ miles} \\ \text{Poland: }&07:50\text{ and }668\text{ miles} \\ \text{Ukraine: }&05:20\text{ and }612\text{ miles}\end{aligned}

Step 2: Convert the times into decimals.

\begin{aligned}\text{France: }&09:10 \equiv 9.17 \\ \text{Germany: }&09:40 \equiv 9.67 \\ \text{Poland: }&07:50 \equiv 7.83 \\ \text{Ukraine: }&05:20 \equiv 5.33\end{aligned}

Step 3: Now use these to calculate the speed of each train.

\begin{aligned}\text{France: }&1093 \div 9.17=\bold{119\text{mph}} \\ \text{Germany: }&820 \div 9.67=85\text{mph} \\ \text{Poland: }&668 \div 7.83 =85\text{mph} \\ \text{Ukraine: }&612 \div 5.33= 115\text{mph}\end{aligned}

Question 13

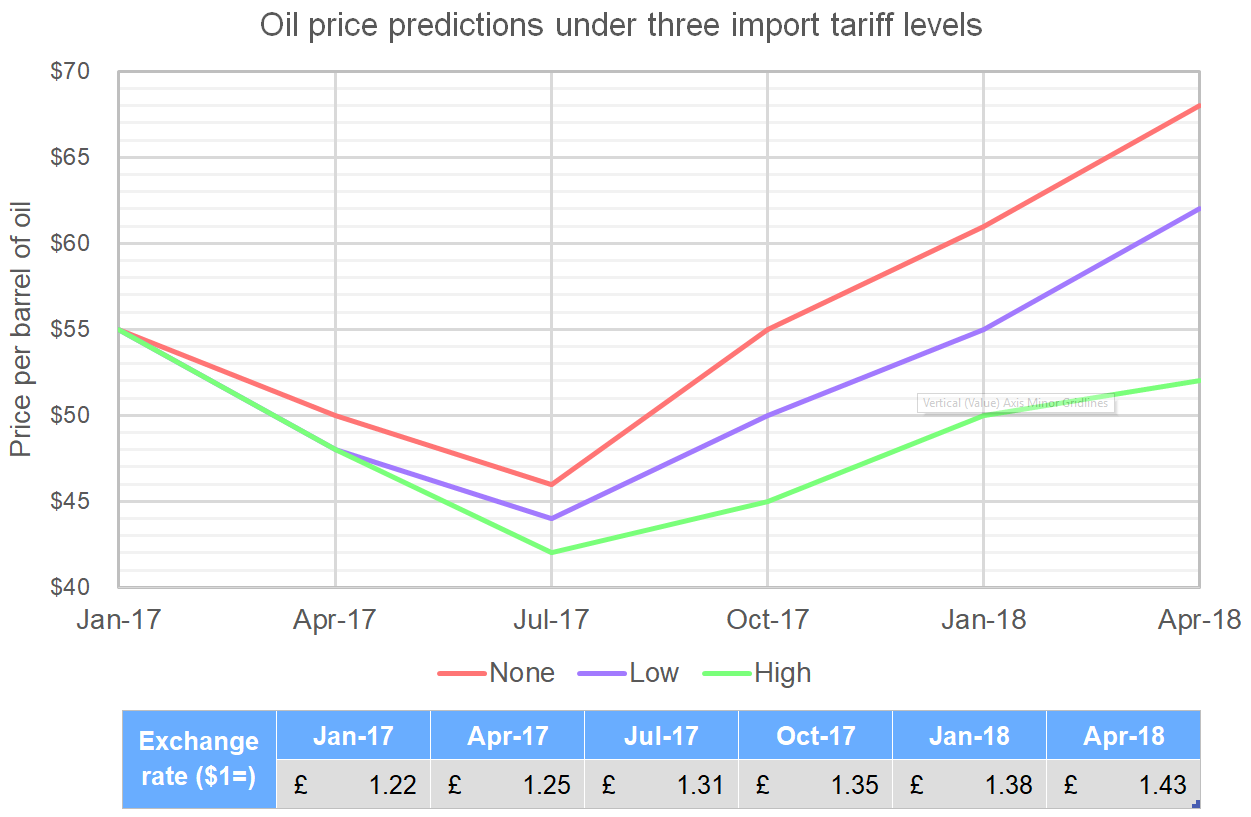
A supplier imports oil and resells it at $59 per barrel. What is the percentage decrease in profit per month from shipping 3000 barrels in July 2017 to shipping 2500 barrels in April 2018 under the highest tariff level?

A: 65.3%

B: 65.7%

C: 66.2%

D: 66.4%

Written Solutions

Step 1: First calculate the initial profit in July under the highest tariff level.

(59\times3000)-(42\times3000)=\$51,000

Step 2: Calculate profit in April.

(59-52)\times2500=\$17500

Step 3: Find the percentage decrease

\dfrac{17500-51000}{51000}\times100=\bold{-65.7\%\text{ or a decrease of 65.7\%}}

Question 14

An investor buys £20,000 worth of oil in January 2017. If this is then sold in January 2018, what is the difference in profit between tariff levels of None and Low in pounds?

A: £2,365.48

B: £2,389.23

C: £2,412.88

D: £2,467.44

Written Solutions

Step 1: First convert the £20,000 into dollars.

\pounds20,000 \div 1.22 = \$16,393.44

Step 2: Use the amount in dollars to buy as many whole barrels of oil in January 2017. Under both tariff levels this is the same.

\$16,393.44 \div 55 = 298\text{ barrels}

Step 3: Sell the 298 barrels in January 2018 and find the difference in price in dollars.

(298\times61)-(298\times55)=\$1,788

Now convert the amount in dollars back into pounds according to the exchange rate in January 2018.

\$1,788\times1.38=\bold{\pounds2,467.44}

Question 15

Calculate the percentage change in price from July 2017 to April 2018 for each of the three tariff types. Express these as a ratio in the simplest form and to 2dp.

A: 1.96: 1.72: 1

B: 1.89: 1.62: 1

C: 2.03: 1.87: 1

D: 1.85: 1.61: 1

Written Solutions

Step 1: Calculate the percentage increase for each tariff.

\begin{aligned}\text{None: }&\dfrac{67-46}{46}\times100=46.65\% \\ \text{Low: }&\dfrac{62-44}{44}\times100=40.91\% \\ \text{High: }&\dfrac{52-42}{42}\times100=23.81\%\end{aligned}

Step 2: Express this as a ratio, then divide through by the lowest value to simplify.

46.65\%: 40.91\%: 23.81\%

\dfrac{46.65}{23.81}: \dfrac{40.91}{23.81}: 1

\bold{1.96: 1.72: 1}

Question 16

45% of the price of a barrel of oil goes to the supplier, while the rest goes to distribution. £10 and £15 are then added to the supplier price under low and high tariffs respectively. What is the difference in the price per barrel that the supplier takes in October 2017 between low and high tariffs?

A: $1.42

B: $1.45

C: $1.48

D: $1.51

Written Solutions

Step 1: Find 45% of each of the low and high tariff prices in October 2017.

\begin{aligned}\text{Low: }&0.45 \times50 = \$22.50 \\ \text{High:}&0.45\times45=\$20.25\end{aligned}

Step 2: Now add on the extra while converting into dollars by dividing by the exchange rate.

\begin{aligned}\text{Low: }&\$22.50+(\pounds10 \div 1.35)=\$29.91 \\ \text{High: }&\$20.25+(\pounds15 \div 1.35)=\$31.36\end{aligned}

Step 3: Find the difference.

\$31.36-\$29.91=\bold{\$1.45}

Question 17

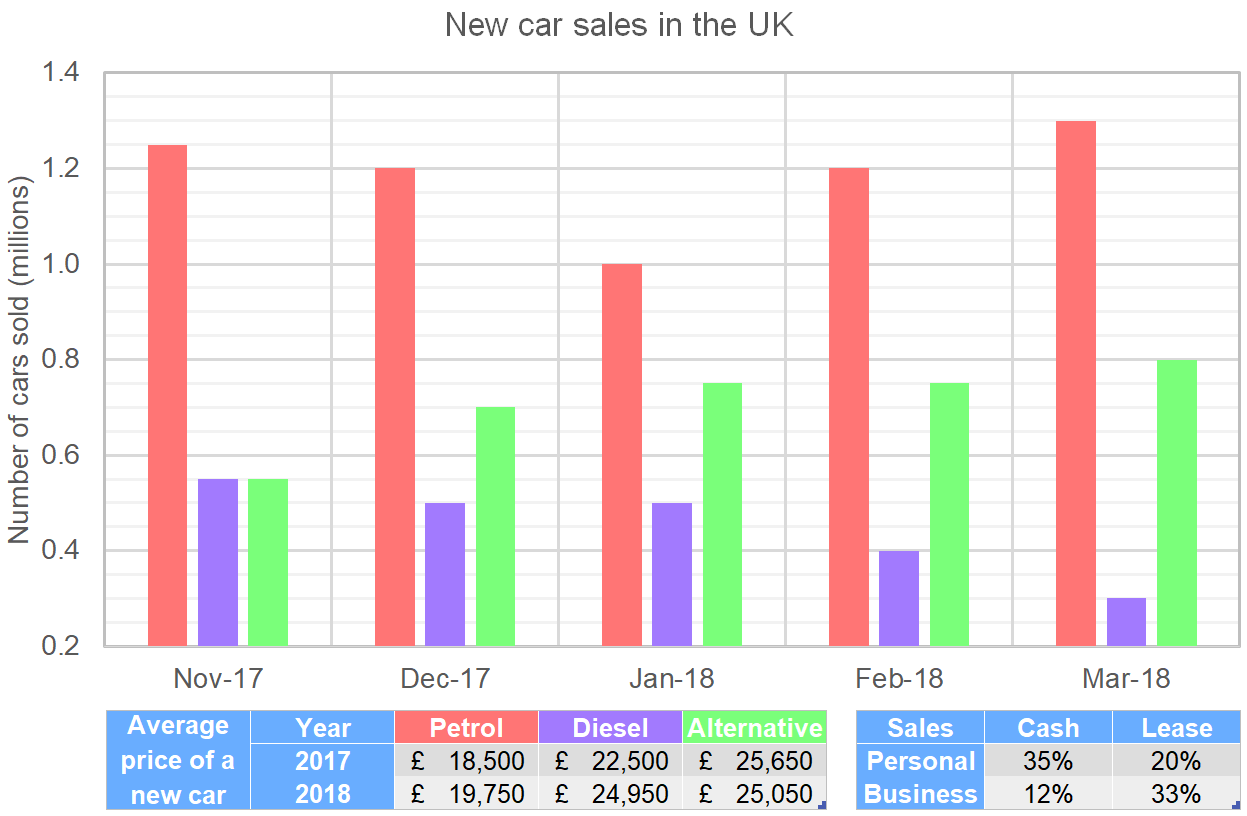
Estimate the percentage change in total value of new petrol cars sold over the whole of 2017 and the whole of 2018. Give your answer to 2dp.

A: 1.61%

B: 1.63%

C: 1.65%

D: 1.67%

Written Solutions

Step 1: Make an estimate for 2017. We only have two months, so we will need to multiply the total by 6 to estimate for the whole year.

(1.25+1.2)\times18,500\times6=\pounds271,950\text{m}

Step 2:  Make the same estimate for 2018. We need to multiply by four to make an estimate for the whole year.

(1+1.2+1.3)\times19,750\times4=\pounds276,500\text{m}

Step 3: Find the percentage change between the years.

\dfrac{276,500-271,950}{271,950}\times100=\bold{1.67\%}

Question 18

What is the ratio of overall revenue generated by sales of each of the three car types for the last two months of 2017? Give your answers to 2dp.

A: 1.85: 1: 1.31

B: 1.90: 1: 1.35

C: 1.92: 1: 1.36

D: 1.95: 1: 1.39

Written Solutions

Step 1: Add up the total number of sales for each type of car in 2017.

\begin{aligned}\text{Petrol: }&1.25+1.2=2.45\text{m} \\ \text{Diesel: }&0.55+0.5=1.05\text{m} \\ \text{Alternative: }&0.55+0.7=1.25\text{m}\end{aligned}

Step 2: Now multiply by the average price of a car in 2017 for each type.

\begin{aligned}\text{Petrol: }&2.45\text{m}\times\pounds18,500=\pounds45,325\text{m} \\ \text{Diesel: }&1.05\text{m}\times\pounds22,500=\pounds23,625\text{m} \\ \text{Alternative: }&1.25\text{m}\times\pounds25,650=\pounds32,062.5\text{m}\end{aligned}

Step 3: Express these as a ratio and simplify.

\pounds45,325\text{m}: \pounds23,625\text{m}: \pounds32,062.5\text{m}

\dfrac{45,325}{23,625}: 1: \dfrac{32,062.5}{23,625}

\bold{1.92: 1: 1.36}

Question 19

Between January and March, what was the difference between the number of personal sales of diesel and business sales of alternative fuel?

A: 375,000

B: 365,000

C: 361,000

D: 345,000

Written Solutions

Step 1: Add up the total number of sales for both diesel and alternative.

\begin{aligned}\text{Diesel: }&0.5+0.4+0.3=1.2\text{m} \\ \text{Alternative: }&0.75+0.75+0.8=2.3\text{m}\end{aligned}

Step 2: Now find the percentage of each that can be attributed to Personal and Business.

\begin{aligned}\text{Diesel: }&0.55 \times 1.2\text{m} = 0.66\text{m} \\ \text{Alternative: }&0.45\times2.3\text{m}=1.035\text{m}\end{aligned}

Step 3: Find the difference

1.035\text{m}-0.66\text{m}=\bold{0.375\text{m}}

Question 20

A company sold 12 alternative fuel cars on a lease for business use in November 2017. If this is indicative of their usual sales, how many cars could they expect to sell total in March 2018?

A: 157

B: 156

C: 155

D: 154

Written Solutions

Step 1: 12 cars account for 33% of the cars sold in November for this company. We expect them to have sold 12 x 3 = 36 alternative fuel cars in total in November 2017.

Step 2: The ratio of sales in November for Petrol: Diesel: Alternative is

\begin{gathered}1.25: 0.55: 0.55 \\ ?: 36: 36\end{gathered}

We know diesel is the same number of cars as alternative since the ratios are the same. To calculate the number of petrol cars we need to first divide by 0.55 and then multiply by 1.25.

(36 \div 0.55)\times1.25\approx82

So, in total 154 cars are sold in November.

Step 3: Calculate the percentage increase in overall UK sales from November to March and use this to calculate an estimate for cars sold by the company in March.

\dfrac{2.4-2.35}{2.35}\times100=2.13\%

1.0213\times154=\bold{157\text{ cars}}